Flappy bird¶
У популарној игри Flappy Bird птица лети и не сме да додирне препреку. Игра је реализована тако што се птица налази стално у средини екрана (хоризонтално). Корисник управља птицом помоћу једног тастера тастатуре тако што је притиском на тај тастер подиже горе (она иначе стално пада на доле). Реализуј ову игру помоћу PyGame. Птичицу представи кругом, а препреке правоугаоницима који се спуштају са врха екрана наниже и са дна екрана навише. Између свака два пара правоугаоника треба да постоји пролаз кроз који се птица може провући. Програм се искључује у тренутку када птица дотакне препреку.
Централни део задатка чини провера да ли се наша лоптица сударила са правоугаоником. Круг сече правоугаоник ако и само ако јој се центар налази унутар правоугаоника или сече неку од његових ивица. Правоугаоници који чине наше препреке су постављени тако да су им све четири ивице паралелне координатним осама (две ивице су вертикалне, две су хоризонталне).
Размотримо прво како ћемо одредити да ли круг сече неку од вертикалних ивица препреке (с обзиром на природу игре, биће довољно проверавати само судар са левом вертикалном ивицом сваког правоугаоника). Нека је центар круга тачка O са координатама (cx,cy) и нека му је полупречник једнак r. Нека су темена вертикалне ивице правоугаоника тачке A са координатама (x,y1) и тачка B са координатама (x,y2). Јасно је да је пресек могућ само ако и само ако се довољно приближила тој ивици и није се превише удаљила од ње. Пресек може да постоји ако и само ако је хоризонтално растојање између центра круга и вертикалне праве на којој се налази дуж мање или једнако r тj. пресек може да постоји акко важи |cx−x|≤r тј. x−r≤cx≤x+r. Ако се cx налази у интервалу [x−r,x+r] пресек може, али не мора да постоји – то зависи од y-координате центра cy. Јасно је да пресек сигурно постоји ако се cy налази у висини дужи (између y1 и y2), међутим, могуће је да је центар мало изнад или мало испод висине дужи, а да пресек и даље постоји.
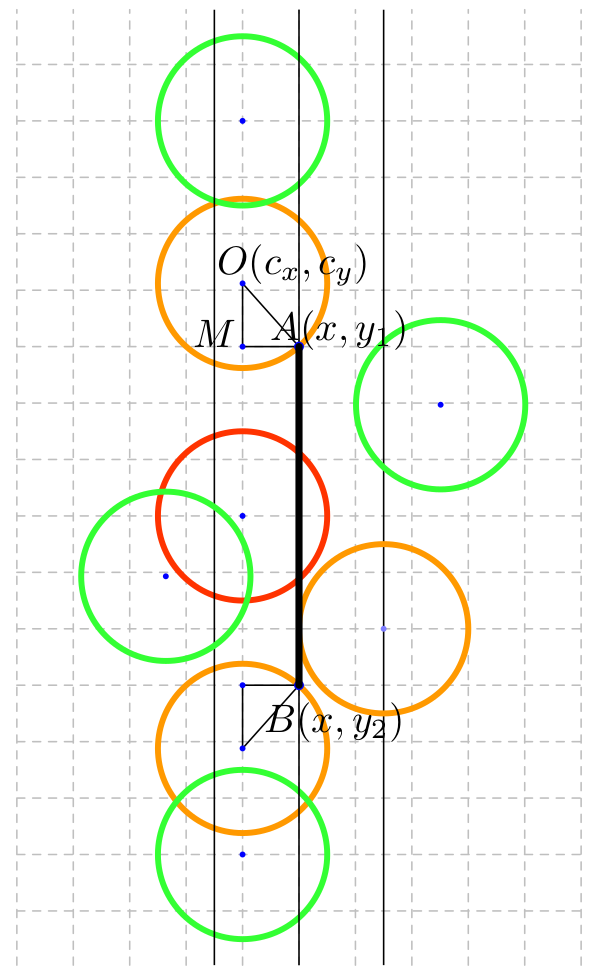
Одредимо које су то граничне висине на којима се круг и дуж секу. Горњи гранични положај је онај у којем круг само додирује дуж тј. садржи тачку A. Означимо са M тачку која представља пројекцију тачке A на вертикалну праву која садржи центар круга O. Троугао AOM је правоугли, са хипотенузом OA и катетама OM и MA. На основу Питагорине теореме важи да је |OA|2=|OM|2+|MA|2. Пошто A лежи на кругу, знамо да је |OA|=r. Такође, знамо да је |MA|2=(cx−x)2. На основу тога, можемо да израчунамо да је |OM|=√r2−(cx−x)2. Дакле, гранична висина центра cy изнад које круг престаје да сече дуж је y1−|OM| тј. y1−√r2−(cx−x)2. На веома сличан начин можемо одредити да је доња гранична висина једнака y2+√r2−(cx−x)2.
Дакле, потребан услов да би круг секао дуж је да важи да cx припада интервалу [x−r,x+r], а ако то важи, онда је потребан и довољан услов пресека то да се cy налази у интервалу [y1−d,y2+d], где је d=√r2−(cx−x)2.
Продискутујмо још и то да услов да cx припада интервалу [x−r,x+r] увек обезбеђује да је поткорена величина ненегативна. Заиста, важи да је |cx−x|≤r, па отуда следи да је (cx−x)2≤r2.
def krugSeceVertikalnuDuz(cx, cy, r, x, y1, y2): if abs(cx - x) > r: return False d = math.sqrt(r**2 - (cx - x)**2) return y1 - d <= cy and cy <= y2 + d(krugsecevertikalnuduz)
Потребно је још одредити да ли лоптица сече хоризонталну ивицу препреке. То би се могло урадити веома сличном анализом претходној, чиме би се добио наредни кôд.
def krugSeceHorizontalnuDuz(cx, cy, r, x1, x2, y): if abs(cy - y) > r: return False d = math.sqrt(r**2 - (cy - y)**2) return x1 - d <= cx and cx <= x2 + d(krugsecehorizontalnuduz)
Међутим, можемо и једноставније, ако анализу пресека круга са хоризонталном дужи успемо да сведемо на проблем пресека са вертикалном дужи. Пошто изометрије чувају инциденцију важи да круг сече дуж ако и само ако се њихове слике добијене применом неке изометријске трансформације секу. Потребно је да пронађемо неку изометријску трансформацију која хоризонталну дуж пресликава у вертикалну. Једна од најједноставнијих таквих је осна симетрија око праве y=x. Том трансформацијом се произвољна тачка (x,y) пресликава у тачку (y,x). Круг са центром у тачки (cx,cy) полупречника r се пресликава у круг са центром у тачки (cy,cx) такође полупречника r. Хоризонтална дуж са теменима (x1,y) и (x2,y) пресликава се у вертикалну дуж са теменима (y,x1) и (y,x2). Стога се пресек са хоризонталном дужи може веома једноставно испитати на следећи начин.
def krugSeceHorizontalnuDuz(cx, cy, r, x1, x2, y): return krugSeceVertikalnuDuz(cy, cx, r, y, x1, x2)(krugsecehorizontalnuduzopt)
Сада можемо веома једноставно дефинисати функцију која проверава да ли се круг и правоугаоник секу.
def tackaPripadaPravougaoniku(x, y, x1, y1, w, h): return x1 <= x and x <= x1 + w and \ y1 <= y and y <= y1 + hdef krugSecePravougaonik(cx, cy, r, x1, y1, w, h): return tackaPripadaPravougaoniku(cx, cy, x1, y1, w, h) or \ krugSeceVertikalnuDuz(cx, cy, r, x1, y1, y1 + h) or \ krugSeceVertikalnuDuz(cx, cy, r, x1 + w, y1, y1 + h) or \ krugSeceHorizontalnuDuz(cx, cy, r, x1, x1 + w, y1) or \ krugSeceHorizontalnuDuz(cx, cy, r, x1, x1 + w, y1 + h)(krugsecepravougaonik)
Препреке чувамо у листи. Свака је препрека уређен пар два правоугаоника. Сваки правоугаоник је одређен четворком бројева који представљају координате његовог горњег левог темена, ширину и висину. У сваком кораку анимације све препреке померамо надесно (тако што пролазимо кроз листу препрека и умањујемо све x координате горњих левих темена правоугаоника). Ако се прва препрека у низу померила испред левог краја прозора, избацујемо је из низа. Ако се последња препрека у низу померила довољно од десног краја прозора, на крај низа убацујемо нову препреку са насумично одређеним положајем пролаза. У сваком кораку такође проверавамо и да ли птица сече неки од правоугаоника који сачињавају препреке и ако сече неки, искључујемо програм. Реагујемо на догађаје тастатуре и када детектујемо притисак на дугме, умањујемо y координату птице (тако подижемо птицу навише). Иначе, у сваком кораку анимације птицу спуштамо мало наниже.
import random, mathimport pygame as pgimport pygamebg# inicijalizujemo rad biblioteke PyGamepg.init()# Podrazumevano, kada se pritisne taster tastature, generise se samo jedan dogadjaj KEY_DOWN, a dogadjaj# KEY_UP se generise nakon otpustanja tastera. Narednim pozivom menjamo to podrazumevano ponasanje.# Prilikom duzeg drzanja tastera generisace se vise dogadjaja KEY_DOWN, a nakon otpustanja tastera generisace# se dogadjaj KEY_UP. Prvi dogadjaj KEY_DOWN se generise cim je pritisnut taster. Nakon toga se ceka broj# milisekundi zadat prvim parametrom funckije set_repeat (ovom slucaju 10), a zatim se naredni dogadjaji# KEY_DOWN generisnu u pravilnim vremenskim intervalima odredjenim drugim parametrom funckije key_repeat# (u ovom slucaju ce se dogadjaji KEY_DOWN generisati na svakih 10 milisekundi, sve dok je taster pritisnut).pg.key.set_repeat(10, 10)# dimenzija prozoradim = (sirina, visina) = (800, 400) # otvaramo prozorprozor = pygamebg.open_window(sirina, visina, "Flappy bird")# da li je nastupio kraj igrekraj_igre = False# parametri ptice koja prolazi kroz prepreke - ona je kruznog oblikaptica_x = sirina // 2ptica_y = visina // 2ptica_r = 30# parametri prepreka koje se pojavljujusirina_prepreke = 60visina_otvora = 130# funkcija generiše dva pravougaonika koji zajedno predstavljaju prepreku kroz koju ptica prolazi# pravougaonici su određeni koordinatama gornjeg levog temena, širinom i visinomdef napravi_prepreku(): vrh_otvora = random.randint(0, visina - visina_otvora) return [[sirina, 0, sirina_prepreke, vrh_otvora], [sirina, vrh_otvora + visina_otvora, sirina_prepreke, visina - vrh_otvora - visina_otvora]]# funkcija kojom se određuje pređeni put tekuće prepreke nakon kojeg se pojavljuje nova preprekadef odredi_rastojanje_nove_prepreke(): # nova prepreka se ne može pojaviti pre nego što je tekuća prešla trećinu širine prozora # a mora se pojaviti nakon što je tekuća prepreka prešla ceo prozor return random.randint(sirina // 3, sirina)# provera da li krug sa datim centrom i poluprečnikom seče vertikalnu duz (x, y1) (x, y2)def krug_sece_vertikalnu_duz(cx, cy, r, x, y1, y2): if cx - r <= x and x <= cx + r: d = math.sqrt(r**2 - (cx - x)**2) if y1 - d <= cy and cy <= y2 + d: return True# provera da li krug sa datim centrom i poluprečnikom seče horizontalnu duć (x1, y) (x2, y)def krug_sece_horizontalnu_duz(cx, cy, r, x1, x2, y): return krug_sece_vertikalnu_duz(cy, cx, r, y, x1, x2)# provera da li krug sa datim centrom i poluprečnikom seče pravougaonik zadat koordinatama# gornjeg levog temena, širinom i visinomdef krug_sece_pravougaonik(krug, pravougaonik): (cx, cy, r) = krug (x0, y0, w, h) = pravougaonik if krug_sece_vertikalnu_duz(cx, cy, r, x0, y0, y0 + h): # provera sudara sa prednjom ivicom return True if krug_sece_horizontalnu_duz(cx, cy, r, x0, x0 + w, y0 + h): # provera sudara sa donjom ivicom return True if krug_sece_horizontalnu_duz(cx, cy, r, x0, x0 + w, y0): # provera sudara sa gornjom ivicom return True return False # proveru sudara sa desnom ivicom preskacemo, jer u igri to nije moguće# krecemo sa jednom pocetnom preprekomprepreke = napravi_prepreku()# odredjujemo kada treba da se pojavi naredna preprekarastojanje_nove_prepreke = odredi_rastojanje_nove_prepreke()def crtaj_scenu(): prozor.fill(pg.Color("white")) # bojimo pozadinu pg.draw.circle(prozor, pg.Color("blue"), (ptica_x, ptica_y), ptica_r) # crtamo pticu for pravougaonik in prepreke: # crtamo prepreke pg.draw.rect(prozor, pg.Color("green"), pravougaonik)def crtaj_kraj(): prozor.fill(pg.Color("white")) # bojimo pozadinu prozora u belo font = pg.font.SysFont("Arial", 60) # font kojim će biti prikazan tekst poruka = "Kraj igre!" # poruka koja će se ispisivati tekst = font.render(poruka, True, pg.Color("black")) # gradimo sličicu koja predstavlja tu poruku ispisanu crnom bojom (sirina_teksta, visina_teksta) = (tekst.get_width(), tekst.get_height()) # određujemo veličinu tog teksta (x, y) = ((sirina - sirina_teksta) / 2, (visina - visina_teksta) / 2) # položaj određujemo tako da tekst bude centriran prozor.blit(tekst, (x, y)) # prikazujemo sličicu na odgovarajućem mestu na ekranu def crtaj(): if not kraj_igre: crtaj_scenu() else: crtaj_kraj() def obradi_dogadjaj(dogadjaj): global ptica_y if dogadjaj.type == pg.KEYDOWN: # strelicom na gore ili razamkom podizemo pticu if dogadjaj.key == pg.K_UP or dogadjaj.key == pg.K_SPACE: ptica_y -= 10def novi_frejm(): global ptica_y, prepreke, rastojanje_nove_prepreke, kraj_igre # ptica pada ptica_y += 3 # prepreke se pomeraju nalevo for pravougaonik in prepreke: pravougaonik[0] -= 3 # proveravamo da li se poslednja prepreka dovoljno pomerila da bi se ubacila nova prepreka if prepreke[-1][0] + prepreke[-1][2] + rastojanje_nove_prepreke < sirina: prepreke = prepreke + napravi_prepreku() # ubacujemo novu prepreku rastojanje_nove_prepreke = odredi_rastojanje_nove_prepreke() # određujemo kada treba da se pojavi naredna prepreka # izbacujemo prepreke koje su ispale sa levog dela prozora while prepreke[0][0] + prepreke[0][2] < 0: prepreke.pop(0) # proveravamo da li je ptica pala na zemlju if ptica_y + ptica_r > visina: kraj_igre = True # proveravamo da li je ptica udarila u neku prepreku for pravougaonik in prepreke: if krug_sece_pravougaonik((ptica_x, ptica_y, ptica_r), pravougaonik): kraj_igre = True sat = pg.time.Clock()kraj = Falsewhile not kraj: crtaj() pg.display.update() for dogadjaj in pg.event.get(): if dogadjaj.type == pg.QUIT: kraj = True else: obradi_dogadjaj(dogadjaj) sat.tick(50) novi_frejm()pg.quit() # isključujemo rad biblioteke PyGame(flappy)