Анализа сложености¶
У претходном поглављу смо видели да је врло корисно знати класу сложености одређеног алгоритма, зато што нам то омогућава да проценимо време његовог извршавања. У овом поглављу ћемо вежбати одређивање сложености алгоритама на једноставнијим примерима.
Један чест тип алгоритма¶
Паскалов троугао
Следећи програм за задато n исписује првих n редова Паскаловог троугла (можете да га испробате). Одредити сложеност алгоритма.
Овде ћемо детаљно анализирати програм и одредити његову сложеност. Када се први пут види, поступак можда делује компликовано, али уз нешто вежбе и стеченог искуства, анализа оваквих програма може се свести на један поглед на код програма.
- Наредбе у прва два реда програма се извршавају по једном (нису у некој петљи) и свака од њих захтева константно време. То значи да је укупна сложеност тог дела програма \(О(1)\).
- Трећи ред програма започиње петљу која се извршава n пута. Све преостале наредбе програма су у тој петљи и то треба имати у виду при одређивању броја операција у наставку програма.
- Наредбе у редовима 4 и 7 се извршавају по једном при сваком проласку кроз петљу по i, што је укупно по n пута, тако да оне доприносе сложености алгоритма са \(О(n)\).
- Наредба print у шестом реду се налази у телу петље из петог реда програма. Због тога се она при сваком проласку кроз спољну петљу (петља по i у трећем реду), извршава онолико пута колико елемената има листа red у том тренутку. Листа је на почетку програма празна, а у сваком проласку кроз петљу по i добија по један елемент. Према томе, листа ће у узастопним проласцима кроз петљу по i редом имати 1, 2, 3 …, n елемената, па ће се и наредба print из шестог реда извршити укупно \(S_n=1+2+3+...+n={ n(n+1) \over 2} = {1 \over 2} n^2 + {1 \over 2} n\) пута, тако да она доприноси укупној сложености алгоритма са \(О(n^2)\), јер у изразу \(S_n\) који представља број извршених операција за шести ред програма, главни (највећи) део је једнак производу константе и \(n^2\).
- Наредба red[k] += red[k-1] у деветом реду је такође у двострукој петљи (као и наредба у шестом реду). Већ смо констатовали да при проласцима кроз спољну петљу листа има редом 1, 2, …, n елемената. Зато ће се при првом проласку кроз спољну петљу ова наредба извршити само за \(k=1\) (дакле једанпут), при другом проласку за \(k=2, k=1\) (два пута), при трећем за \(k=3, k=2, k=1\) итд. То је укупно \(1+2+3+...+n\) извршавања, па као и малопре, па закључујемо да и ова наредба доприноси укупној сложености алгоритма са \(О(n^2)\).
Закључили смо да се програм састоји од неколико делова чије су сложености \(О(n^2)\), \(О(n)\) и \(О(1)\). Како је сложеност \(О(n^2)\) највећа од свих које су се појавиле, остале се могу занемарити, тако да је укупна сложеност алгоритма такође једнака \(О(n^2)\).
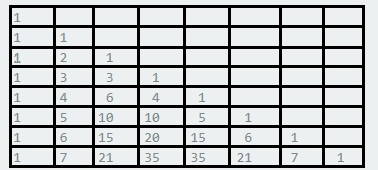
Напомена: при оцењивању сложености алгоритма могу се појавити и суме сложеније од \(S_n\). Није нужно да се свака таква сума тачно израчуна. На пример ако је јасно да се сума изражава полиномом, најчешће је довољно одредтити само степен тог полинома. На примеру суме \(S_n\) било је довољно приметити да је та сума полином другог степена, дакле реда величине \(n^2\). То се може урадити на пример тако што приметимо да је на слици испод попуњена приближно половина од укупно \(n \cdot n\) поља, а то је \(n^2/2\) (у примеру са слике је \(n=8\)).
Варљива двострука петља¶
На основу претходног примера може се помислити да алгоритам који има две уметнуте петље (са једноставним наредбама у телима петљи) има квадратну сложеност. То је често истина, али треба бити опрезан при извођењу закључака. Погледајмо следећи пример.
Провера састављене речи
Замислимо да је неко покушао да од задатих слова састави што дужу реч. Програм који следи, за дата слова и пријављену реч проверава да ли је та реч могла да буде састављена од понуђених слова. Одредити сложеност алгоритма овог програма.
Можете да испробате програм и поиграте се. Можете и да детаљније тестирате програм и проверите да ли исправно ради у разним ситуацијама, али овде нам то чак није ни битно. Бавићемо се само одређивањем сложености овог програма.
У првој табели у претходном поглављу, сортирање је поменуто као пример алгоритма сложености \(O(n \cdot Lg(n))\). Можемо да претпоставимо да и Пајтон функција sorted има управо ту сложеност (као општи метод сортирања теоријски није могуће да буде бржа, а као функција из библиотеке извесно је написана ефикасно па није ни спорија).
Означимо број датих слова са \(N_S\), дужину пријављене речи са \(N_R\), и уведимо ознаку \(N = max(N_S, N_R)\). Користећи ове ознаке, имамо да је сложеност закључно са осмим редом једнака \(O(N \cdot Lg(N))\). Део од реда 14 до краја програма је једноставан и очигледно је сложености \(O(1)\). Позабавимо се сада двоструком петљом, то јест редовима 9 - 12.
- Наредба у реду 11 се (при једном проласку кроз for петљу) извршава све док је слово из састављене речи различито од i-тог задатог слова, али се иде најдаље до последњег понуђеног слова. Ако се једном стигне до последњег понуђеног слова, при наредним пролазима кроз for петљу ће први део услова у while наредби бити одмах нетачан и наредба у реду 11 се неће више извршавати. Из овога закључујемо да је укупан број извршавања наредбе у реду 11 највише \(N_S\), дакле \(O(N_S)\), што се утапа у претходно утврђених \(O(N \cdot Lg(N))\) и може се занемарити (овде „утапа се” значи да је мање сложености, тако да за довољно велико n постаје занемарљиво).
- Наредба у реду 12 се извршава по једном за свако слово у састављеној речи, тако да она доноси \(O(N_R)\), што се такође може занемарити у односу на \(O(N \cdot Lg(N))\).
На основу овог разматрања видимо да је сложеност овог алгоритма одређена сортирањем као најспоријим делом, дакле \(O(N \cdot Lg(N))\).
Скривена сложеност¶
У наредном примеру имамо обрнуту ситуацију, а то је да алгоритам наизглед линеарне сложености заправо има квадратну сложеност.
Цезарова шифра
Сматра се да је римски војсковођа Цезар користио шифроване покуке, како би осигурао тајност преписке. Шифровање се састојало у померању сваког слова за одређени мброј места у латинском алфабету, док се размаци и знаци интерпункције нису шифровали. На пример при померању за три места, слово A се шифрује са D, B се шифрује са E, и тако даље до Z, које се шифрује са C (слова се померају кружно кроз алфабет). За исти померај од три слова у енглеском алфабету, шифра поруке „KOLIKO LJUDI” би била „NROLNR OMXGL”.
Ради једноставности примера, ми ћемо на даље подразумевати да се користи енглески алфабет и да се порука састоји искључиво од великих слова и размака. Одредити сложеност функција f1 и f2 из програма испод, које за дати текст израчунавају шифру.
Очигледно је да је за одређивање сложености функције \(f_1\) критична наредба у једанаестом реду. Ова наредба се извршава по једном за свако слово текста, па делује да је сложеност функције \(f_1\) једнака \(O(n)\), где је n дужина текста.
Грешка у овом закључивању је у томе што једно извршавање ове наредбе захтева време које није константно (а није ни ограничено константом). Наиме, стрингови у језику Пајтон су неизменљиви (енгл. immutable), што значи да се постојећи стринг не може мало изменити, него се мора направити потпуно нови испочетка. То подразумева преписивање свих слова која се већ налазе у постојећем стрингу у нови стринг, затим дописивање најновијег слова шифре у нови стринг, и на крају додељивање тако формираног стринга променљивој sifra. Због тога ова наредба при једном извршавању захтева време сразмерно дужини стринга. Након ове констатације, анализом сличном оној у примеру „Паскалов троугао” (на почетку ове стране), можемо да закључимо да је сложеност функције \(f_1\) заправо квадратна.
За разлику од стринга, листа у језику Пајтон јесте изменљива. Захваљујући томе, наредба у реду 18 се извршава сваки пут у константном времену, тако да укупно доноси сложеност \(O(n)\). Наредбама у редовима 15 и 20 јесте потребно време сразмерно са n, али оне се налазе ван петље, тако да и оне доприносе сложености само са \(O(n)\). Према томе, функција \(f_2\) има линеарну сложеност (нема дела функције који је спорији од \(O(n)\)).
Ово можемо да потврдимо и експериментално:
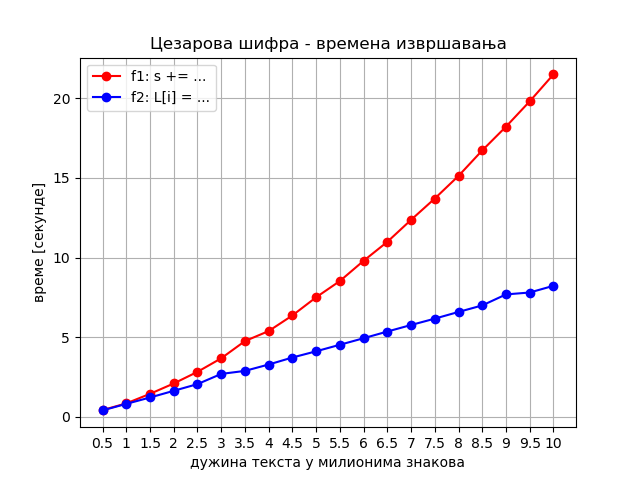
Уколико ова времена извршавања упоредимо са временом извршавања програма линеарне сложености за рачунање сума, видимо да је овде чак и функција линеарне сложености прилично спора (око 5 пута спорија за исто n од програма линеарне сложености који рачуна суме). То можемо да објаснимо чињеницом да је овде коришћена операција рачунања кода једног слова сигурно доста спорија од операције обичног сабирања, коришћене у рачунању сума.
Покушајмо да убрзамо обе функције за рачунање Цезарове шифре тако што ћемо првобитни начин рачунања кода једног слова
да заменимо са
На тај начин се код рачуна само по једном за свако слово алфабета, што је укупно само 26 рачунања (занемарљиво за велико n). Након тога, за свако слово текста који се шифрује, код тог слова се чита из речника. То би требало да буде брже него рачунање кода за свако слово целог текста.
На следећој слици су приказана времена обе функције пре и после промене начина рачунања кода слова.
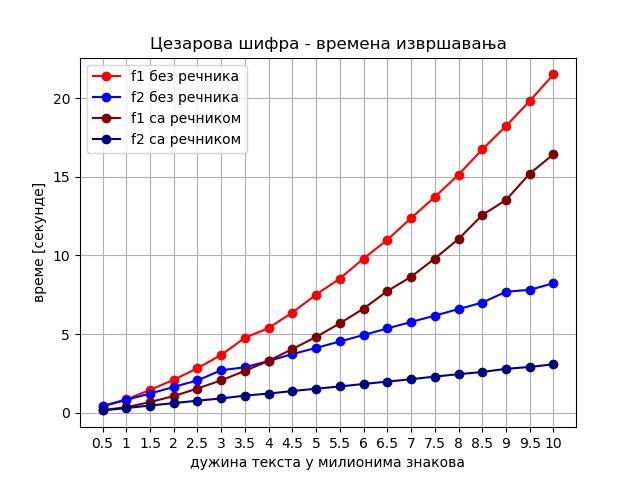
Слика је у складу са очекивањем да се класа сложености обе функције не мења (остаје квадратна за прву, а линеарна за другу функцију), а да обе функције постају брже. У нашем тестирању је на тексту од 10 милиона слова време извршења прве функције смањено са 21.50 на 16.42 секунде, а друге са 8.23 на 3.08 секунди.
Поредећи ова времена, примећујемо да се она нису смањила пропорционално (функције нису убрзане исти број пута), него за отприлике исто време, а то је на тексту од 10 милиона слова за око 5.3 секунди. Ово је тако јер добијено убрзање у првој функцији не утиче на њен најспорији (квадратни) део, у коме се само преписују слова. Убрзано је само додавање новог слова у шифру, а оно се дешава исти број пута у обе функције, па је и временски добитак за ове две функције на истом шифрованом тексту отприлике једнак у секундама.
Констатовали смо да је део алгоритма \(f_1\) који је квадратне сложености (а који потиче од преписивања слова) остао непромењен, а убрзан је само део алгоритма који је линеарне сложености. У одређивању сложености до сада смо занемаривали све осим најспоријег дела алгоритма, то јест оног са највише операција, а он је овде остао исти. Због тога није јасно да ли је уштеда времена у алгоритму \(f_1\) уопште значајна и колико је значајна. Судећи по мерењу (поменути бројеви и слика) делује да је уштеда значајна, а по теоријском разматрању да није.
Да би било јасније шта се дешава, погледајмо како се мења количник времена извршавања алгоритма без употребе речника и са употребом речника (за сваки од алгоритама \(f_1\) и \(f_2\) посебно пратимо мењање количника времена двеју верзија):
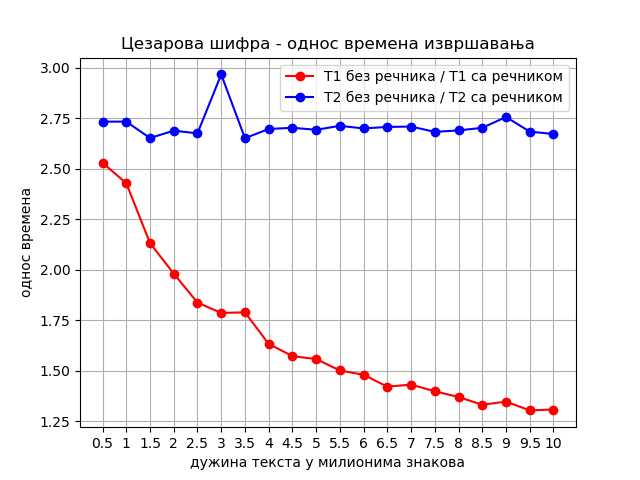
Са графика можемо да прочитамо да је овом променом у коду алгоритам \(f_2\) постао око 2.7 пута бржи за мање-више сваку величину текста који се шифрује, док за алгоритам \(f_1\) не можемо да кажемо колико пута је убрзан. Да бисмо ово опажање формулисали прецизније, уведимо ознаке \(T_1^{sa}\) и \(T_1^{bez}\) за времена рада алгоритма \(f_1\) са и без речника, а \(T_2^{sa}\) и \(T_2^{bez}\) за времена рада алгоритма \(f_2\) са и без речника, редом. Сада за алгоритам \(f_2\) на основу графика можемо да кажемо на пример да је количник \(T_2^{bez} / T_2^{sa}\) већи од 2, док за алгоритам \(f_1\) на основу графика не можемо са сигурношћу да одаберемо неки број \(q > 1\), такав да почев од неког n на даље важи да је количник \(T_1^{bez} / T_1^{sa}\) већи од q.
Може се доказати да такав број q заправо и не постоји за функцију \(f_1\) (а да постоји за \(f_2\)). То значи да се количник \(T_1^{bez} / T_1^{sa}\) толико приближава јединици, да са даљим повећавањем n убрзана верзија алгоритма \(f_1\) (са речником) није ни 1% бржа од основне (без речника). То значи да за још веће вредности n убрзање које смо добили употребом речника за алгоритам \(f_1\) није нарочито значајно, јер са порастом n то убрзање постаје сразмерно све мање (иако у апсолутним износима све веће). Заинтересовани читацои могу да виде доказ ако кликну на дугме, мада је тај доказ мање битан од закључака које овде истичемо.
Током анализе сложености функције \(f_1\) закључили смо да је број (елементарних) операција алгоритма \(f_1\), а тиме и теоријско време рада функције, облика \(P(n) = A n^2 + B n + C\). Нека је број операција за верзију без употребе речника \(P^{bez}(n) = A^{bez} n^2 + B^{bez} n + C^{bez}\), а са употребом речника \(P^{sa}(n) = A^{sa} n^2 + B^{sa} n + C^{sa}\). Током разматрања сложености алгоритма функције \(f_1\) видели смо да квадратни део броја операција потиче од преписивања слова у нови стринг, а тих преписивања има исто, са или без речника. То значи да је \(A^{bez} = A^{sa} = A\), а одатле
\({P^{bez}(n) \over P^{sa}(n)} = {A n^2 + B^{bez} n + C^{bez} \over A n^2 + B^{sa} n + C^{sa}} = {1 + {B^{bez} \over A n} + {C^{bez} \over A n^2} \over 1 + {B^{sa} \over A n} + {C^{sa} \over A n^2}}\)
Када n тежи бесконачности, бројилац и именилац последњег количника теже броју 1, па и сам количник тежи броју 1. Због тога, какав год број q > 1 да изаберемо, за довољно велико n ће бити \(q > {P^{bez}(n) \over P^{sa}(n)} > 1\)
Дакле, израз \(P_1^{sa}\) нема нижу константу уз главни, квадратни члан, него уз линеарни. То је довољно да уштеда у времену буде све већа (и да неограничено расте), али није довољно да би функција \(f_1\) са речником била асимптотски бржа за константан фактор (види терминологију доле).
За функцију \(f_2\) смо утврдили да је њен број операција облика \(P(n) = A n + B\). Нека је број операција за верзију без употребе речника \(P^{bez}(n) = A^{bez} n + B^{bez}\), а са употребом речника \(P^{sa}(n) = A^{sa} n + B^{sa}\). Промена у програму се односи на налажење кода слова, што се обавља за свако од n слова текста, па према томе утиче на линеарни фактор. Зато за функцију \(f_2\) важи \(A^{bez} \neq A^{sa}\), а како је верзија са речником бржа, јасно је да је \(A^{bez} > A^{sa}\). У изразу \({P^{bez}(n) \over P^{sa}(n)} = {A^{bez} n + B^{bez} \over A^{sa} n + B^{sa}} = {A^{bez} + {B^{bez} \over n} \over A^{sa} + {B^{sa} \over n}}\) кад n тежи бесконачности, бројилац последњег количника тежи ка \(A^{bez}\), а именилац ка \(A^{sa}\), па количник тежи ка \({A^{bez} \over A^{sa}} = K > 1\). За довољно велико n ће овај количник бити довољно близу броја K, да ће бити већи од, на пример \(q = {1+K \over 2}\).
Терминологија:
Нека су сложености неких алгоритама А и B редом \(T^A(n)\) и \(T^B(n)\). Ако ове сложености припадају истој класи (на пример \(O(n^3)\)), кажемо да алгоритми A и B имају исту асимптотску сложеност.
Ако при истој асимптотској сложености за неко фиксирано \(q > 1\), почев од неког n важи \({T^A(n) \over T^B(n)} > q\), кажемо да је алгоритам B асимптотски бржи бар за константан фактор од алгоритма A. У жаргону се каже и да алгоритам B има нижу константу од алгоритма A.
Користећи уведену терминологију, можемо да кажемо да:
- Две верзије функције \(f_2\) (са и без употребе речника) имају међусобно исту асимптотску сложеност, и то \(O(n)\).
- Две верзије функције \(f_1\) (са и без употребе речника) имају међусобно исту асимптотску сложеност, и то \(O(n^2)\).
- Функција \(f_2\) са употребом речника има нижу константу него без речника.
- Функција \(f_1\) са употребом речника јесте бржа него без речника, али не за константан фактор (нема нижу константу), иако разлика времена између две верзије Функције \(f_1\) неограничено расте са повећавањем n.
Напомена: Овде смо се бавили само одређивањем и поређењем сложености датих функција и њихових варијација, а не и налажењем што ефикаснијег решења. Иначе, у Пајтону постоје знатно ефикаснији начини да се текст шифрује на тражени начин. Један пример је функција f3 (коју ако желите, можете да испробате у свом Пајтон окружењу). Ова функција је линеарне сложености (решење мање сложености није могуће јер треба проћи кроз цео текст), али са много нижом константом него функција f2 због знатно ефикаснијег обављања потребних операција.

