Мерење времена у програму¶

У овом поглављу се не бавимо налажењем најефикаснијег решења за постављени задатак, него само на примеру показујемо како време рада програма зависи од његове структуре. Видећемо како може да се приближно измери време рада програма, како различити програми могу да се упореде по брзини и како у једноставним случајевима може да се процени време извршавања програма.

Следе два програма на Пајтону који исписују тражене суме.

Први програм рачуна суме у главном програму и исписује их током израчунавања:

Други програм има дефинисану функцију \(suma(n)\), која рачуна суму првих n природних бројева. Затим се у главном програму исписује вредност те функције за свако i од 1 до n:

Можете да испробате програме и видите да дају исти, тражени резултат. Судећи по томе, изгледа да је свеједно на који од ова два начина ћемо написати програм и користити га. Испоставиће се, међутим, да између ова два програма постоји значајна разлика у времену потребном за њихово извршавање.

Како да одредимо колико је времена потребно програму да се изврши?

За већину програмских језика је довољно једноставно пронаћи на интернету упутства. Поступак се углавном своди на програмско очитавање тренутног времена непосредно пре и после оног дела програма чије трајање нас интересује, а затим исписивање разлике тих времена. На Пајтону то можемо да урадимо овако:

Подсећамо, ако желите да испробате програм за неко веће n, боље је да програм прекопирате и сачувате у фајл на на вашем рачунару и извршите га ван веб браузера.

Следеће питање које можемо себи да поставимо је:

Како да стекнемо неки осећај о томе колико времена треба програму за које n?

Једна ствар коју можемо одмах да урадимо је да позовемо израчунавање суме за разне вредности n, а затим те вредности n и времена потребна за израчунавање суме испишемо у облику табеле:

Програм може на пример да испише овакав извештај (времена могу бити и друкчија):

n =  1000000, rezultat:    500000500000, vreme     0.16 sekundi
n =  2000000, rezultat:   2000001000000, vreme     0.31 sekundi
n =  3000000, rezultat:   4500001500000, vreme     0.49 sekundi
n =  4000000, rezultat:   8000002000000, vreme     0.65 sekundi
n =  5000000, rezultat:  12500002500000, vreme     0.83 sekundi

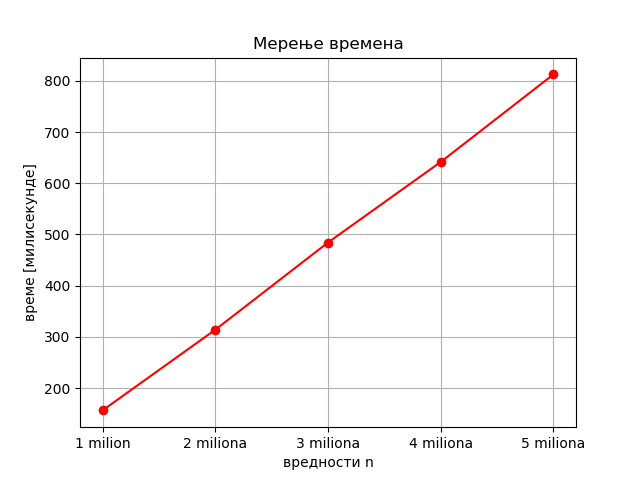
Већ одавде се види да су времена приближно сразмерна вредностима n, на пример \(0.16 : 1000000 \approx 0.31 : 2000000 \approx 0.49 : 3000000\) итд.

Још прегледнији начин да уочимо ову пропорционалност је приказивање графика времена израчунавања суме у зависности од n.

Напомена: Програме који су овде коришћени као помоћни алат (за мерење времена, цртање графика и слично), можете да видите ако кликнете на одговарајуће дугме. Они нису главна тема овог излагања и није неопходно да их разумете, чак није неопходно ни да их погледате да бисте испратили излагање. Они су дати су само ради комплетности, за случај да некога интересује како се овакве анализе могу обављати.

Добија се слика попут ове:

Ова приближна пропорционалност времена израчунавања са вредностима n се могла и очекивати, јер да би израчунао суму, програм треба да изврши n операција сабирања s += i (и наредбу s = 0 пре тога, што је занемарљиво јер је n велико).

Како овај програм за дато \(n\) извршава \(n+1\) наредбу, он јесте линеарне сложености. Користећи ту чињеницу, можемо (прилично прецизно) да проценимо колико би времена требало програму на пример за \(n=20~000~000\). Како је програм за \(n=5~000~000\) радио око 0.83 секунди, за 4 пута веће n можемо очекивати \(4*0.83s = 3.32s\).

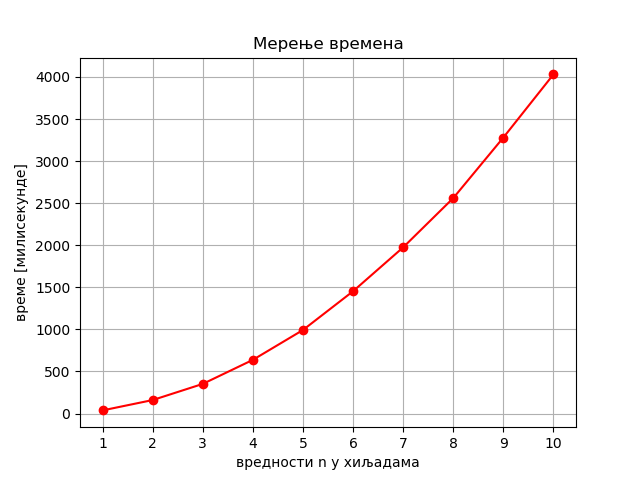
Погледајмо сада како изгледа график времена израчунавања суме за други наведени алгоритам, који користи функцију suma. Након мало испробавања, видимо да је овај програм знатно спорији, па ћемо за вредности n бирати мање бројеве (1000 до 10000 уместо 1000000 до 5000000 као у претходном случају).

Добијена је слика:

а програм исписује

n =     1000, rezultat:          500500, vreme    31.24 ms
n =     2000, rezultat:         2001000, vreme   156.25 ms
n =     3000, rezultat:         4501500, vreme   359.35 ms
n =     4000, rezultat:         8002000, vreme   633.19 ms
n =     5000, rezultat:        12502500, vreme   993.25 ms
n =     6000, rezultat:        18003000, vreme  1448.38 ms
n =     7000, rezultat:        24503500, vreme  1984.94 ms
n =     8000, rezultat:        32004000, vreme  2547.53 ms
n =     9000, rezultat:        40504500, vreme  3291.45 ms
n =    10000, rezultat:        50005000, vreme  4049.11 ms

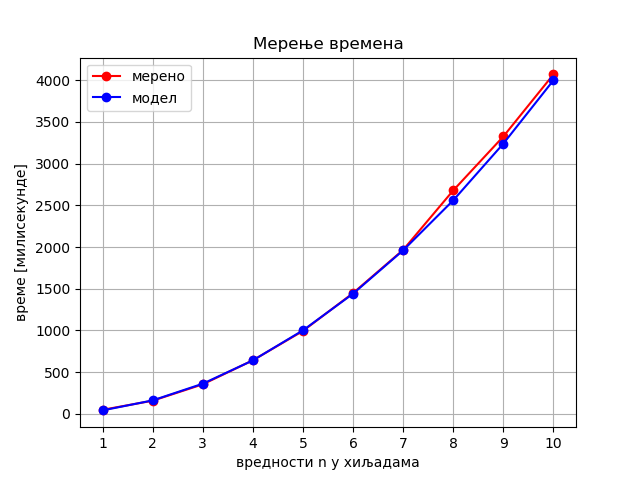
Примећујемо да ова зависност није линеарна. Када се n удвостручи, време рада постаје отприлике 4 пута веће (на пример за \(n=2000\) добијамо време 156.25 ms, док за \(n=4000\) одговарајуће време 633.19 ms). Слично томе, за три пута већи улазни податак, време је приближно 9 пута веће. Одавде можемо да претпоставимо да је време израчунавања \(t\) за овај алгоритам приближно сразмерно са \(n^2\). Ако израчунамо \(t/n^2\) за разне \(n\), видимо да су вредности количника углавном око 0.00004. Доцртајмо уз график времена израчунату функцију \(f(n)=0.0004*n^2\) као модел стварне функције потрошеног времена, да бисмо видели колико ова функција - модел и стварно време рада алгоритма одступају једно од другог:

Добијамо слику:

Овим смо (експериментално) установили да је време рада другог алгоритма (наведен је испод поново) приближно квадратна функција од n. То би значило да је и број извршених операција приближно сразмеран са \(n^2\). Због чега је то тако?

За било које дато i, функција suma(i) извршава приближно i операција. Пошто се функција позива за свако i од 1 до n, то се у функцији укупно изврши \(1+2+...+n = n(n+1)/2 = n^2/2 + n/2\) операција. Када томе додамо иницијализације и исписивања, добијамо да је број извршених операција нека функција облика \(an^2+bn+c\), где су \(a, b, c\) константе.

Напоменимо да у овом програму спорост не долази од саме употребе функције. Позив функције можемо да схватимо као једну веома брзу операцију, чији је утицај на укупно време извршавања веома мали, тако да организовање кода у функције практично никада не угрожава ефикасност. Овде се далеко највећи део времена троши на поновна сабирања, која су могла да буду избегнута. На пример, након што је израчунао \(S_{999~999}\), овај програм рачуна \(S_{1~000~000}\) поново сабирајући од 1, уместо да искористи претходно израчунату суму.

За прву функцију смо видели да јој за \(n=5~000~000\) треба око 0.83 секунде, а другој за \(n=10~000\) треба око 4 секунде. Јасно је да је друга функција доста спорија, али било би лепо видети времена ових функција на истом графику, да би било јасније колико је спорија. То међутим, није једноставно, јер за \(n\) реда 50000, друга функција је неудобно спора (за 5 пута веће n потребно је приближно 25 пута више времена, па можемо проценити да би тој функцији требало око \(25 \cdot 4s \approx 100s\)), док би се график прве функције једва „одлепио” од x-осе (време рада прве функције је приближно пропорционално са n, па би јој требало око \(0.83s / 100 \approx 0.008s\)).

Додајмо зато још једну функцију, која ће представљати прву функцију успорену 1000 пута:

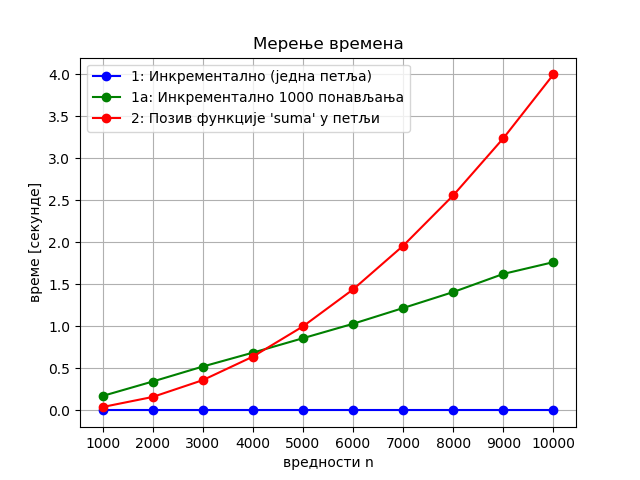
Времена извршавања у секундама (на 3 децимале):

f1(n):        0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
f1_x1000(n):  0.172 0.344 0.522 0.687 0.859 1.031 1.219 1.409 1.625 1.765
f2(n):        0.040 0.160 0.360 0.640 1.000 1.440 1.960 2.560 3.240 4.000

Као што смо и претпостављали, прва функција (представљена плавом бојом) је сувише брза да би њено приказивање било корисно за вредности n до 10000. Њена успорена верзија (на слици представљена зеленом бојом) наравно такође има линеарну сложеност, јер линеарна функција помножена са 1000 је и даље линеарна. Ово једноставно закључивање је потврђено и сликом (мала одступања од праве линије настају углавном због разних других програма који раде у позадини на истом рачунару).

Шта би било за неко веће n?¶

Алгоритам представљен зеленом линијом можемо замислити као први (најбржи) алгоритам који се извршава на 1000 пута споријем рачунару (или језику). Видимо да и тако успорен, алгоритам линеарне сложености већ за \(n>5000\) постаје бржи од другог, чија је сложеност квадратна (црвена линија). Одавде је јасно да за веће улазне податке постаје много важније која је сложеност алгоритма, него колико брзо се програм извршава.

То што алгоритам квадратне сложености за \(n=10~000\) ради само пар секунди дуже од једног или другог линеарног алгоритма не треба никога да завара. За веће вредности улаза, предност линеарног алгоритма над квадратним постаје много израженија. На пример, за \(n=5~000~000\):

• како програм квадратне сложености за \(n=10~000\) ради око 4 секунде, за \(n=5~000~000\) можемо да проценимо време на \((5~000~000/10~000)^2 * 4s = 1~000~000s\), што је нешто преко 11 и по дана.
• време успореног другог програма можемо проценити на \(1000 * 0.83s = 830s < 14\) минута, (без успорења, програм је радио око \(0.83s\))

Закључак: за \(n=5~000~000\), чак и 1000 пута успорени алгоритам линеарне сложености би био преко 1000 пута бржи од алгоритма квадратне сложености, док би оригинални алгоритам линеарне сложености био преко милион пута бржи од квадратног!

Напомена: На такмичењима из програмирања се тест примери често праве „економично”, то јест тако да буду што мањи, али довољно велики да ухвате разлику између линеарног и квадратног алгоритма. Та разлика у времену извршавања онда делује неубедљиво (на пример само пола секунде преко лимита) и неосвајање свих поена за квадратни алгоритам изгледа неправедно. Имајући у виду претходни пример (11 дана према 0.83 секунде), јасно је да овакви приговори нису оправдани.