Променљиве¶
Променљиве су један од најважнијих концепата у програмирању. У овом поглављу упознаћемо различите типове променљивих. Показаћемо како се на позорници могу пратити промене вредности променљивих преко монитора који им се придружују.
Шта је променљива?
Променљива (варијабла) је именована област меморије рачунара. Можемо да кажемо да је променљива попут именоване кутије у којој програм привремено чува податке са којима ради.
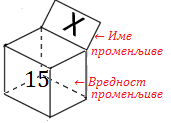
Променљива на слици има име Х, а њена текућа вредност је 15.
Променљиве могу чувати једну вредност, на пример број или слово. То су просте променљиве. Међутим, постоје и сложене променљиве које чувају више вредности, на пример низ слова (стринг) низ бројева, низ речи, … У Скречу се овакав низ назива листа.
Ми смо у претходним пројектима користили неименоване вредности. Текст „Здраво свете“ и сви остали које смо уносили у блокове Изговори и Замисли су подаци – стрингови (низови знакова).
Бројеви које смо уносили као аргументе у наредбе кретања (иди, усмери се, промени за) су вредности које се могу сместити у променљиве.
Услов понављања и услов гранања може да има две вредности – тачно и нетачно, дакле и то је вредност, логичка вредност.
За сложеније програме које будемо писали биће нам потребно да именујемо неке вредности, то јест да уведемо променљиве.
Како се креирају променљиве?
У групи наредби Подаци на почетку нема блокова (сл. а). Потребно је прво креирати променљиву кликом на дугме Направи променљиву.
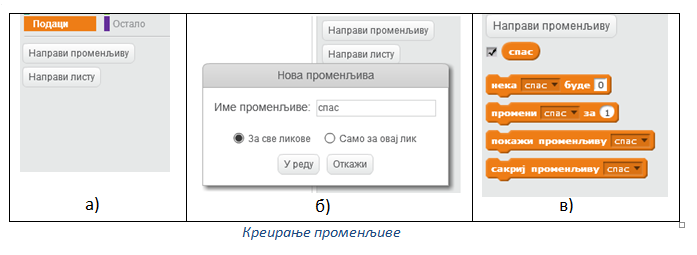
Кликом на ово дугме отвара се дијалог за креирање нове променљиве.
Променљива може бити локална, само за скрипте придружене активном објекту (лику или позорници) или глобална.
Глобалне променљиве могу да користе сви објекти пројекта. Уписом имена променљиве и кликом на дугме У реду у палети блокова појављују се блокови за 4 наредбе и репортер са именом променљиве уз који стоји дугме за потврду (слика в).
Блокови који представљају променљиве називају се репортери зато што обавештавају колика је текућа вредност променљиве. Репортери се појављују у два облика и могу да се поставе само у отворе истог облика на блоковима наредби.
Репортери са заобљеним крајевима (елипсе) садрже бројеве или стрингове и могу да се поставе у блокове који имају заобљену белину.
Репортери шестоугаоног облика садрже логичке податке (тачно или нетачно) и могу да се поставе у блокове са одговарајућим отвором.
Неки репортерски блокови имају и поље за потврду. Ако се кликне на поље за потврду, на позорници се појављује монитор у коме се приказује текућа вредност променљиве. Монитор може да приказује вредности променљивих у више различитих формата приказаних на следећој слици.

мали приказ вредности са именом променљиве,
велики приказ вредности без припадајућег имена,
са клизачем који омогућава промену вредности променљиве.
Прелазак из једног у други формат постиже се двокликом на монитор. Формат са клизачем може се користити једино за променљиве које креира корисник. Десним кликом на клизач подешавају се минимална и максимална вредност.
 Проучи следеће примере пројеката¶
Проучи следеће примере пројеката¶
У претходном поглављу као пример 5 анализирали смо пројекат Лов. То је игра за два
играча. Сваки играч диркама са тастатуре води своју мачку и покушава да улови миша.
Миш се појављује на случајним позицијама на екрану. Кад год га нека од мачака додирне,
миш се скрива и појављује на следећој случајној позицији.
Надоградићемо овај пројекат тако што ћемо увести 2 променљиве: Играч 1 и Играч 2 које ће
чувати број поена играча. Сваки додир миша рачунаће ће се играчу који води мачку која га
је дотакла као поен. Ова евиденција ће се водити у скрипти за миша, а број поена оба
играча моћи ће да се прати на екрану.
Такође ћемо увести и променљиву Време која треба да ограничи време игре.
Пример 1 - Надоградња пројекта Лов¶
Дакле, да би се могли пратити поени играча, обе променљиве Играч 1 и Играч 2 треба да буду чекиране и да њихови монитори буду приказани у првом формату.
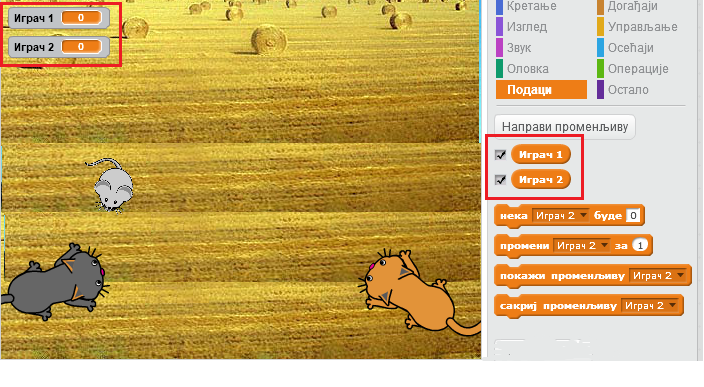
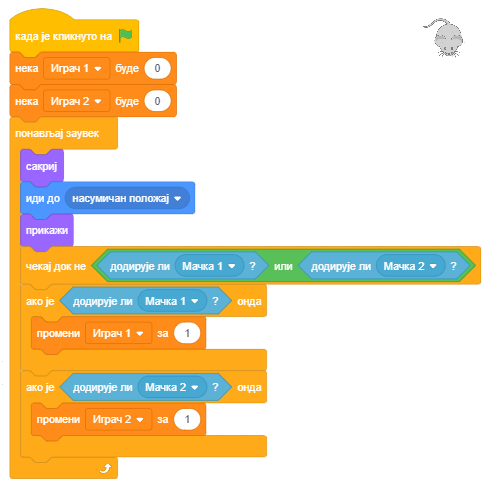
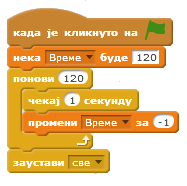
На почетку скрипте за миша треба поставити њихове почетне вредности на 0. Приликом сваког додира мачке треба повећати број поена. Тако сада скрипта за миша има следећи изглед.
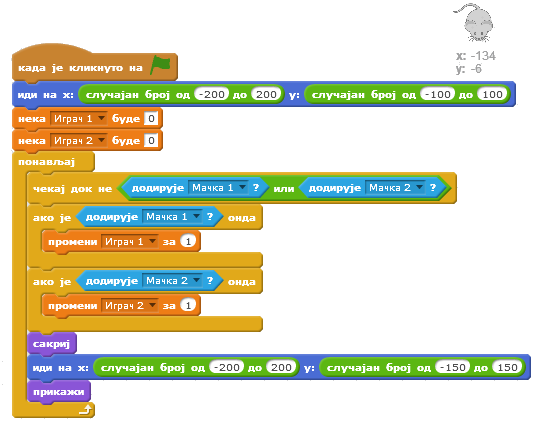
Остаје још да додамо ограничење времена за игру. То ћемо учинити тако што ћемо у скрипти која се покреће кликом на зелену заставицу поставити вредност проенљиве
Време на жељено трајање игре, на пример 120 секунди. Затим ћемо у циклусу који се понавља 120 пута извршавати наредбу 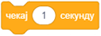 и смањивати вредност променљиве за 1.
По изласку из циклуса поставићемо наредбу
и смањивати вредност променљиве за 1.
По изласку из циклуса поставићемо наредбу  . И ову скрипту придружићемо мишу.
. И ову скрипту придружићемо мишу.
За следећи пример искомбиноваћемо један од Скречових почетних пројеката: игру maze_starter и пројекат Лавиринт.
Пример 2 - Игра Лавиринт2¶
У пројекту Лавиринт задатак је да се лик Mouse 1 проведе кроз компликован лавиринт. Излаз из лавиринта налази се на врху позорнице, па је услов да се игра успешно заврши да координата у лика буде већа од 180. Лик се води диркама са стрелицама. Ако удари у неки од зидова лавиринта који су црне боје, враћа се на полазну позицију.
У нашем ремиксу кретање миша ће се прецизније контролисати. Један притисак на дирку стрелица води га само 3 корака (а не 10 као у изворном пројекту). Ударац у зид лавиринта неће се кажњавати враћањем на почетак, већ само одбијањем од зида као у maze starter пројекту (иде -2 корака). Пошто је миш врло често при окретању репом ударао о зидове, одсекли смо му реп (у едитору слика прво се реп селектује алатком преобликуј, па се избрише кликом на дирку Del).
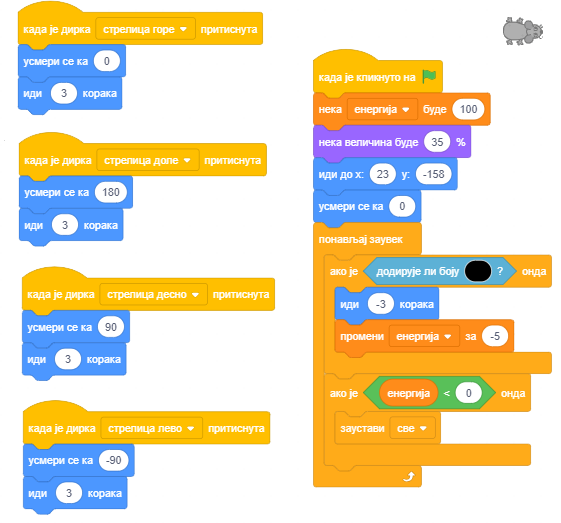
Овако измењене скрипте за миша приказане су на следећој слици.
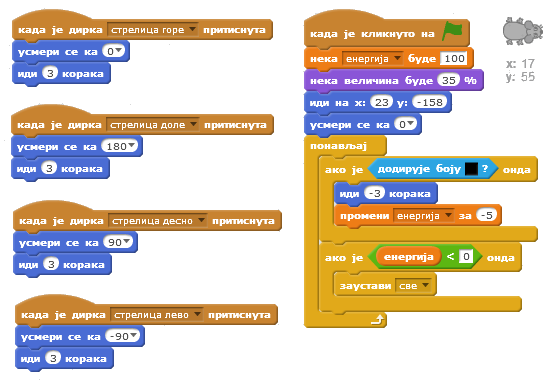
Међутим, игра није лакша, јер миш мора да избегава непријатеље: 2 отровне лоптице и духа лавиринта.

Лоптице се, као и миш, одбијају од зидова лавиринта, док дух може да пролази кроз зидове.
Миш на почетку има 100 јединица енергије која се сваким ударом о зид лавиринта смањује за 5, а додир непријатеља је још опаснији. Судар са лоптицом одузима 10 јединица енергије, а судар са духом 50.
Игра се успешно завршава ако миш стигне до излаза из лавиринта, а неуспешно ако у лавиринту остане без енергије.
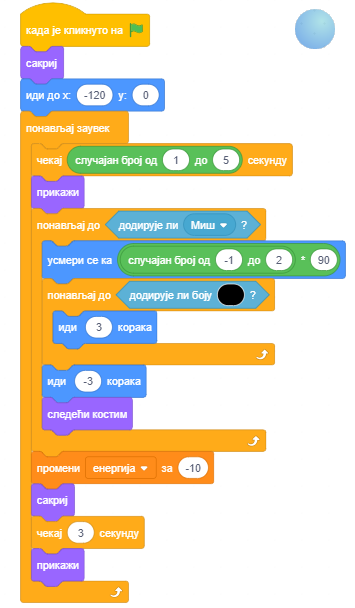
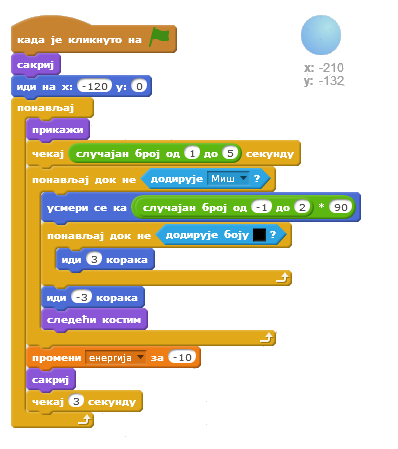
Понашање лоптице
Лоптица је на почетку игре сакривена. Појављује се после 1 до 5 секунди од почетка игре, Лоптица 1 на позицији (-120,0), а Лоптица 2 на (165,55).
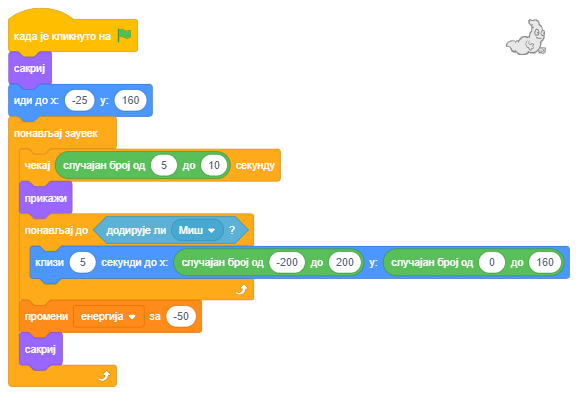
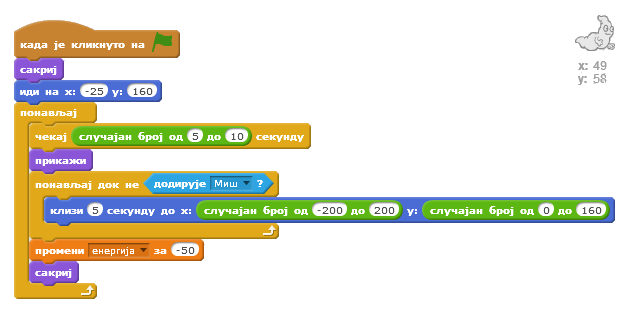
Понашање духа
Дух је на почетку игре такође сакривен. Појављује се после 5 до 10 секунди. Све док не додирне миша клизи по 5 секунди до случајно изабране позиције у горњој половини лавиринта. Ако додирне миша одузима му 50 поена енергије, сакрива се и после чекања 5 до 10 секунди појављује се и понавља претходно описано кретање.
Следи пример пројекта који може да се користи као образовни програм за предшколце и
ученике нижих разреда основне школе који уз игре на рачунару уче да рачунају. Погодан
је зато што мало старији ђаци кроз његово пројектовање и надоградње могу да добију идеје
како да решавају сложеније математичке проблеме.
Пројекат Мали математичар представља ремикс пројекта Математик.
Пример 3- Пројекат Мали_математичар¶
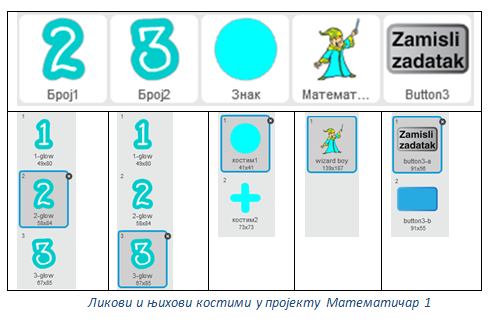
У чаробној земљи живе мали чаробњак Математичар, Број1, Број2 и Знак аритметичке операције. Сваки Број има 3 костима у облику бројева распоређених у строгом поретку - 1, 2, 3. Знак има 2 костима у облику знакова аритметичких операција: * и +.
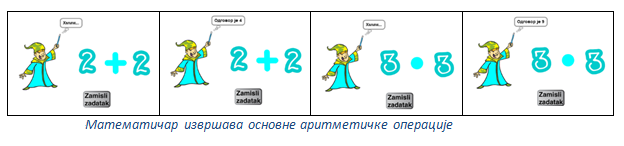
Бројеви и Знак воле да играју игру Примери: при сваком клику на дугме Постави задатак они на случајан начин, као кад неко баца новчић, бирају свој костим. Како год да се мењају Бројеви и Знак у примерима, Математичар их без грешке сабира и множи.
Не зна се тачно који чаробњак га је томе научио, али прича се да Математичар трага за мајстором који би га научио да дели и одузима.
Тајна Математичара састоји се у томе да сваки костим има не само име и слику него и редни број. То је обичан број, с којим се могу извршавати математичке операције.
Математичару је довољно да сазна који је редни број костима изабран у примеру за сваки Број и Знак.
Пошто смо већ видели да репортери знају све, Математичару је довољно да узме потребне репортере из групе Осећаји, блок потпуног гранања aко онда
из групе Управљање, логички оператор једнакости и математичке операторе множења и сабирања из групе Операције.
За почетак ћемо креирати пројекат Математичар 1 у коме ће у корисник кликом на дугме замисли постављати задатак, а мали чаробњак га решавати.
Креирање ликова
За лик математичара изаберите дечака чаробњака Wizard Boy из библиотеке ликова, а за лик Број1 цифру 1-Glow, такође из библиотеке ликова. Затим ћемо у картици Костими увести још два костима за Број1 и то прво цифру 2-Glow, а затим цифру 3- Glow. Лик Број2 направићемо као умножак лика Број1. Оба костима за лик Знак нацртаћемо у едитору слика (Круг за множење и знак + за сабирање). Дугме Замисли задатак направићемо од дугмета button-3 коме на првом костиму треба да дописати текст „Zamisli zadatak“.
Сценарио и скрипте за ликове
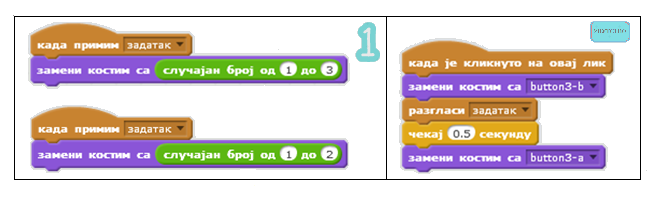
На екрану лево стоји мали чаробњак, а десно један поред другог Број1, Знак и Број2. Дугме Замисли задатак налази се на дну екрана. Програм се покреће кликом на дугме Замисли задатак које тада шаље поруку „задатак”. На поруку задатак реагују сви остали ликови: математачар тако што замишља „Хммм…“, а бројеви и знак тако што се показују у случајно изабраном костиму. Кликом на математичара појављује се стрип облачак са резултатом задате операције. Ликови Број1, Број2 и Знак имају само по једну скрипту – реакцију на догађај Кад примим поруку задатак са једном једином наредбом – Замени костим са случајан број од 1 до 3 (1 до 2 за Знак). Лик дугме реагује само када се кликне на њега. Тада мења костим (да се зна да је на њега кликнуто), шаље поруку, чека пола секунде и враћа се у првобитни изглед. Скрипте придружене бројевима и дугмету приказане су на следећој слици.
Скрипте које описују понашање математичара када прими поруку „задатак” и када се кликне на њега приказане су на следећој слици.
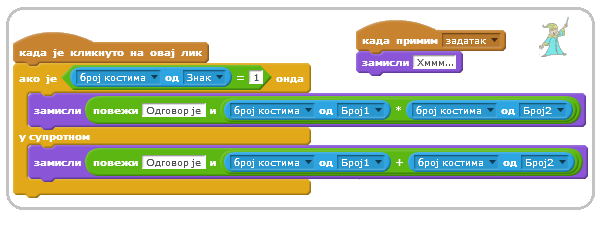
Задржимо се на другој скрипти математичара. Када се кликне на њега, он замишља резултат, а ево како долази до њега.
Као што смо рекли Знак се може појавити у два костима: Први костим – костим са редним бројем 1 одговара множењу, па ако је случајно генерисан број 1 математичар треба да помножи бројеве.
Ако за знак није генерисан број 1, онда математичар треба да сабере бројеве. Слично, редни бројеви костима за Број1 и Број2 одговарају самим бројевима са којима математичар треба да изврши назначену операцију.
У тексту који се појављује у стрип облачцима користили смо операцију повежи.
Операција  је једна од операција која се може извршити над подацима типа стринг (ниска знакова).
Она од две ниске знакова прави јединствену која садржи све знакове прве ниске на коју се надовезују сви знакови друге ниске.
На пример, извршавањем блокова са слике лево, ако се на питање „Како се зовеш?” одговори са „Никола”, Мачак ће изговорити „Здраво Никола”.
је једна од операција која се може извршити над подацима типа стринг (ниска знакова).
Она од две ниске знакова прави јединствену која садржи све знакове прве ниске на коју се надовезују сви знакови друге ниске.
На пример, извршавањем блокова са слике лево, ако се на питање „Како се зовеш?” одговори са „Никола”, Мачак ће изговорити „Здраво Никола”.

Како се функцијски блокови умећу у функцијске блокове
У нашој скрипти придруженој математичару поставили смо у поље за аргумент наредбе замисли операцију повежи. У прво поље операције повежи уписали смо текст „Одговор је „, а у друго поље операцију * (помножи), односно + (сабери). Затим смо у прво поље аритметичке операције унели број костима лика Број1, а у друго број костима лика Број2. Да ли је ово објашњење јасно?
Ако нисте сигурни како да ово урадите, погледајте детаљније објашњење
У поглављу Циклуси направили смо класификацију блокова који се користе у Скречу и указали да се тзв. Функцијски блокови умећу у тзв. Командне блокове. Како правимо сложеније пројекте тако користимо и све сложеније функцијске блокове који се образују од више других функцијских блокова, као у примеру који управо описујемо. Зато ћемо овом приликом сликом показати корак по корак како се формира сложени аргумент наредбе замисли. При том идемо уназад, с краја на почетак. Треба да добијемо:
Треба да добијемо 
Како да добијемо
 и
и  ?
?
а) Узмемо блок  из групе блокова Осећаји.
из групе блокова Осећаји.
б) Из листе ликова коју добијемо кликом на троуглић уз лик Математичар изаберемо Број1 (односно Број2) в) Из листе променљивих придружених овом лику коју добијемо када кликнемо на троуглић уз променљиву место х изаберемо број костима
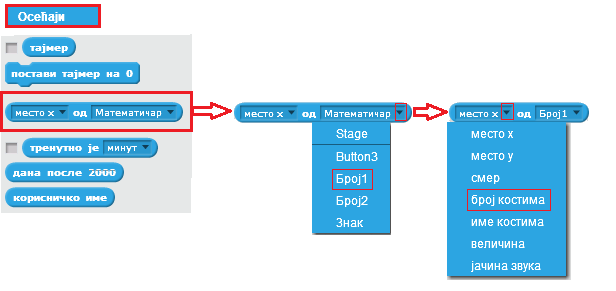
Како да добијемо

а) Узмемо блок  из групе блокова Операције
из групе блокова Операције
б) Поставимо први аргумент који смо добили по опису 1 у прво поље 
в) Поставимо други аргумент који смо добили по опису 1 у друго поље
Како да добијемо

а) Узмемо блок  из групе блокова Операције
из групе блокова Операције
б) Упишемо текст „Одговор је ” у прво поље 
в) Поставимо аргумент који смо формирали по опису 2 у друго поље
Коначно, овако формиран аргумент поставимо у поље блока

Прва надоградња у пројекат Математичар 2
Пројекат Математичар 2 ради са бројевима од 1 до 9. За надоградњу је потребно ликовима Број1 и Број2 додати костиме са редним бројевима 4 до 9 (редом цифре од 4-Glow до 9-Glow) и у њиховим скриптама у наредби замени костим са случајан број уместо „од 1 до 3“ поставити од „1 до 9“.
Друга надоградња у пројекат Математичар3
У овом пројекту реакција малог чаробњака на поруку задатак треба да буде постављање одговарајућег питања кориснику, а потом саопштавање да ли је одговор тачан или није. Није потребно обрађивати догађај клик на лик математичара. Треба додати и објашњење како се програм користи.
То можемо регулисати увођењем још једног дугмета на коме пише Упутство. Када се кликне на ово дугме шаље се порука „упутство” на коју реагују позадина и математичар. Позадина се мења у Позадина2 на којој је исписано упутство за употребу програма, а математичар се смањује на 30% своје величине како не би заклањао упутство.
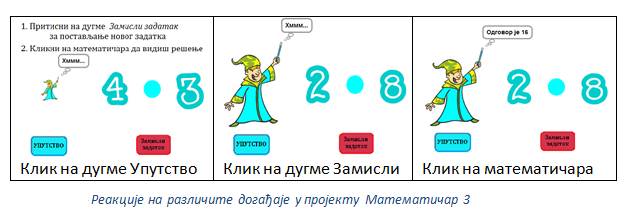
У поглављу Процедуре можете видети и четврту надоградњу пројекта Мали математичар у којој се осим сабирања и одузимања појављују и операције множење и дељење.
Пројекат 4 - Погоди мој број¶
Краљ у краљевству Осмица имао је 8 кћери. Када је дошло време да се његова мезимица, најмлађа принцеза уда упитао је каквог би младића желела за мужа.
Принцеза је одлучила да ће за будућег мужа изабрати паметног младића који успе да реши све загонетке које пред њега постави.
Прва од њих је била да са што мање питања погоди који број од 1 до 100 је замислила.
На питање које би поставио кандидат одговарала је са: Мој број је мањи, Мој број је већи или Браво, погодио си.

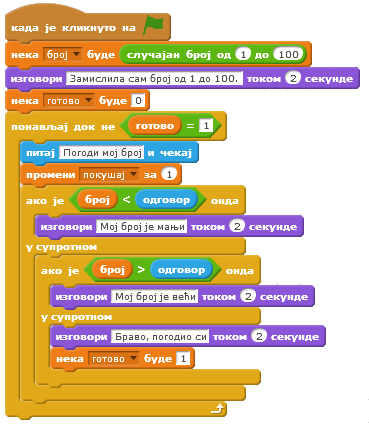
Надоградња у пројекат Погоди мој број2
Принцези је учитељ математике рекао да паметним постављањем питања мора да се дође до одговора у највише 7 покушаја, па је принцеза одлучила да у ужи избор уђу само кандидати који из највише 7 покушаја погоде који број је замислила.
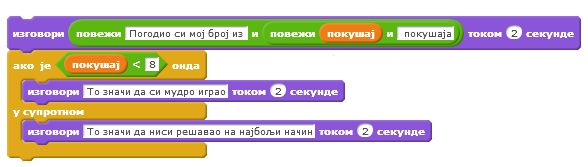
Да бисмо направили пројекат у коме принцеза поред провере да ли је њен број погођен броји и из колико покушаја је то урађено, направићемо још једну променљиву покушај. Њену вредност ћемо повећавати за 1 приликом сваког преузимања одговора корисника.
Тако ћемо по изласку из циклуса тражења одговора имати евиденцију после колико питања је корисник успео да погоди замишљен број. Принцеза ће, пошто каже из колико је покушаја број погођен, рећи и То значи да си мудро играо ако је број покушаја мањи од 8, односно То значи да ниси решавао на најбољи начин ако је број покушаја 8 или већи.
 Одговори на следећа питања¶
Одговори на следећа питања¶
Бројевни изрази
Питање 1¶
Да ли изрази  и
и  имају исту вредност (да/не)?
имају исту вредност (да/не)?
Питање 2¶
- ниједан
- 10/(-1)=-10
- први
- 5-3=2
- други
- оба
- Изрази имају различите вредности.
Q-1: Који од израза  и
и  има негативну вредност?
има негативну вредност?
Питање 3¶
Колика је вредност израза 
Питање 4¶
- 45
- 10/(-1)=-10
- 11
- 5-3=2
- 15
Q-2: Колика је вредност израза  ?
?
Питање 5¶
- 3
- 10/(-1)=-10
- 11
- 5-3=2
- 6
Q-3: Колика је вредност израза  ?
?
Питање 6¶
- 8
- 10/(-1)=-10
- 14
- 5-3=2
- 13
Q-4: Колика је вредност израза 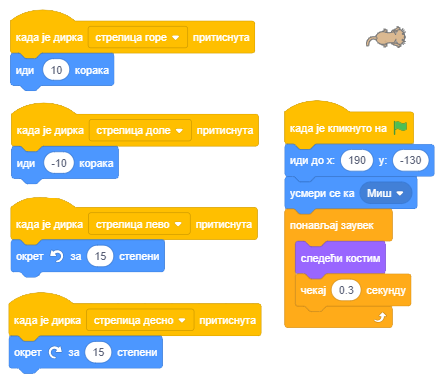 ?
?
Питање 7¶
- 22
- 10/(-1)=-10
- 35
- 5-3=2
- 19
- 235
- Изрази имају различите вредности
Q-5: Колика је вредност израза 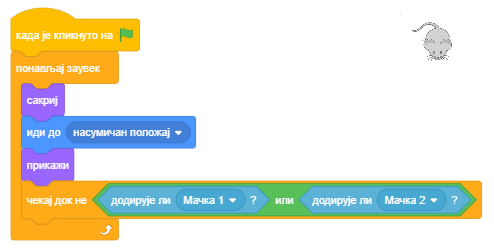 ?
?
Питање 8¶
- 0
- 10/(-1)=-10
- 4
- 5-3=2
- 20
- 29
- Изрази имају различите вредности
Q-6: Колика је вредност израза  ?
?
Променљиве
Питање 9¶
Питање 10¶
Питање 11¶
Питање 12¶
Питање 13¶
Питање 14¶
-
Q-8: Поређај наредбе тако да променљиве а и b размене вредности.
Покушај поново
- нека pom буде a
- 1
- нека a буде b
- 2
- нека b буде pom
- 3
Питање 15¶
Питање 16¶

- a=5
- Није тачно да је 5<5, услов гранања није испуњен.
- a=0
- 0<5.
- a=10
- Није тачно да је 10<5, услов гранања није испуњен.
- a=4
- 4<5.
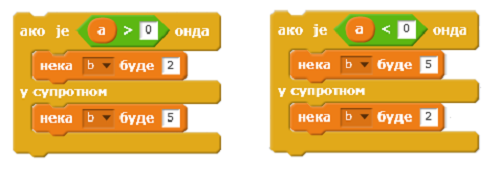
Q-10: За које вредности променљиве а ће променљива b добити вредност 1? (Изабери све тачне одговоре).
Питање 17¶
Питање 18¶
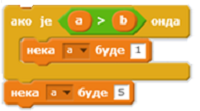
Коју вредност ће имати променљива a после извршења наредбе условног преласка ако су претходно вредности променљивих а и b биле: a=2 и b=4?
Коју вредност ће имати променљива a после извршења наредбе условног преласка ако су претходно вредности променљивих а и b биле: a=4 и b=2?
Питање 19¶
Питање 20¶
Питање 21¶
- b=5
- b=2
- Услов гранања је испуњен, па се полазна вредност променљиве увећава.
- b=6
- b=3
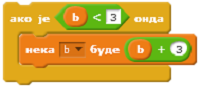
Q-13: Коју вредност ће имати променљива b после извршења наредбе условног преласка ако је претходно вредност променљиве b била b=2?
- b=5
- b=2
- b=6
- Услов гранања није испуњен, па се полазна вредност променљиве не мења.
- b=3
Q-14: Коју вредност ће имати променљива b после извршења наредбе условног преласка ако је претходно вредност променљиве b била b=3?
Питање 22¶

- a=5
- a=1
- Услов гранања је испуњен, па се полазна вредност променљиве увећава прво за 2 па још за 3.
- a=10
- a=6
Q-15: Коју вредност ће имати променљива a после извршења наредбе условног преласка ако је претходно вредност променљиве а била а=1?
- а=5
- а=1
- а=10
- Услов гранања није испуњен, па се полазна вредност промењиве не мења.
- a=6
Q-16: Коју вредност ће имати променљива a после извршења наредбе условног преласка ако је претходно вредност променљиве a била a=5?
Питање 23¶
-
Q-17: Превлачењем упари почетне вредности променљивих са вредностима по извршењу наредбе условног преласка.
Покушај поново
- a=2 b=4
- a=2 b=3
- a=2 b=2
- a=2 b=1
- a=4 b=2
- a=1 b=2
- a=4 b=0
- a=-1 b=0
Питање 24¶
-
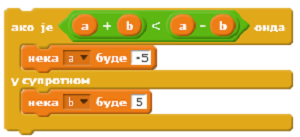
Q-18: Превлачењем упари почетне вредности променљивих са вредностима по извршењу наредбе условног преласка.
Покушај поново
- a=2 b=1
- a=2 b=5
- a=2 b=-2
- a=-5 b=-2
- a=-2 b=1
- a=-2 b=5
- a=-2 b=-1
- a=-5 b=-1
Питање 25¶
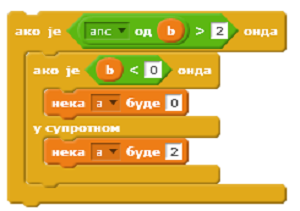
- а=5
- Испуњен је услов грања прве наредбе, вредност а се мења.
- а=0
- а=2
- Оба услова гранања су испуњена.
Q-19: Коју вредност ће имати променљива a после извршења наредбе условног преласка ако су претходно вредности променљивих биле a=5 и b=-3?
Питање 26¶
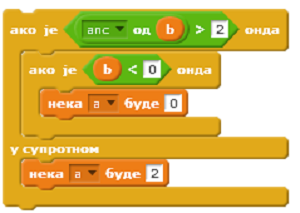
- а=5
- а=0
- Није испуњен услов гранања друге наредбе.
- а=2
- Испуњен је услов гранања прве наредбе.
Q-20: Коју вредност ће имати променљива a после извршења наредбе условног преласка ако су претходно вредности променљивих биле a=5 и b=3?
Питање 27¶

- само за а=6
- само за а=-6
- Није испуњен услов гранања друге наредбе.
- за свако а које није цело
- ни за једно а
Q-21: За коју вредност променљиве a ће се променљивој b доделити вредност 3?
Питање 28¶
Питање 29¶
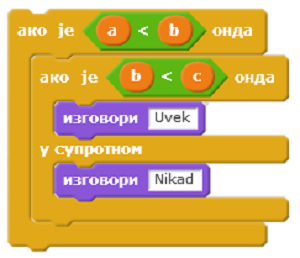
- a < b и b > c
- Шта ако је b=c?
- a < b и b >= с
- a > b
- У случају a>b уопште се не проверава услов у другој наредби гранања.
- а >= b
- У случају a>=b Уопште се не проверава услов у другој наредби гранања.
Q-23: Под којим условом лик изговара Nikad ?
Питање 30¶
- не више од 2
- увек 3
- зависи од вредности а и b
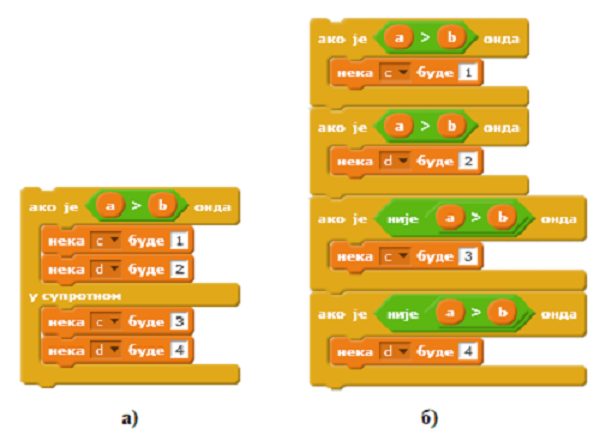
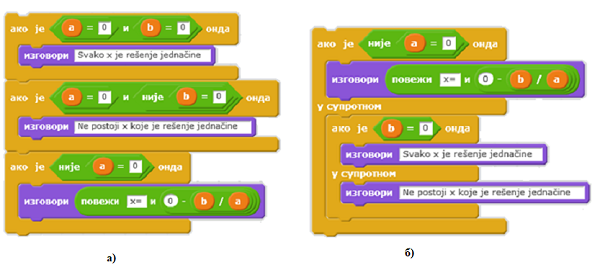
Q-24: Колико наредби гранања се извршава у програмском сегменту а) ?
- Оба кода раде исправно.
- Тачно.
- Други сегмент није исправан.
- Нетачно.
- За неке вредности a и b су равноправни и по брзини и по тачности.
- Нетачно.
- Други сегмент увек ради брже од првог.
- Тачно.
Q-25: Сегменти програма а) и б) треба да исписују решење линеарне једначине ax + b = 0. Које реченице су тачне? (Изабери све тачне одговоре)
Питање 31¶
- Увек је довољно 4 питања.
- Тачно.
- Увек је потребно 4 питања.
- Нетачно.
- Понекад је могуће одредити број и са мање од 4 питања
- Нетачно.
- Број потребних питања зависи од замишљеног броја.
- Нетачно.
Q-26: Петар је замислио цео број од 0 до 15. Програм исписује питања облика „да ли је замишљени број мањи од …“, док не добије довољно података, а затим исписује замишљени број. Ако је програм написан тако да ГАРАНТУЈЕ теоријски минималан број питања, онда важи: (Изабери све тачне одговоре)
 Покушај¶
Покушај¶
Вежба 1¶
Напиши низ наредби који:
размењује вредности две променљиве;
одређује који је број већи од два броја која се уносе са улаза;
одређује минимум три броја који се уносе са улаза.
Вежба 2¶
Вежба 3¶
Напиши програм у коме се понавља следећи низ корака:
лик тражи од корисника да унесе природан број и затим изговара
који број је претходник,
који број је следбеник,
који број је двоструко већи и
који број је двоструко мањи од унетог броја.
Понављање прекинути када корисник унесе број 0.
Вежба 4¶
Напиши програм у коме се понавља следећи низ корака:
лик тражи од корисника да унесе два цела броја х и у различита од нуле и затим изговара
збир бројева „х” и „у” је „х+у”,
разлика бројева „х” и „у” је „х-у”,
производ бројева „х” и „у” је „х*у” и
количник бројева „х” и „у” је „х/у”.
при чему уместо променљивих наведених под знацима навода треба да стави њихове вредности.
Понављање прекинути када корисник унесе број 0 било као вредност х, било као вредност у.
Вежба 5¶
Дат је израз 16 : 8 : 4 : 2. Колика је његова вредност? Запиши га у Скречу и провери.
Дописивањем два пара заграда на различите начине, добијају се изрази са различитм вредностима. Одреди све могуће вредности које се на тај начин могу добити.
За сваки од начина запиши израз у Скречу и провери да ли си добро израчунао његову вредност.
Помоћ. Дописивањем заграда добијају се следећи изрази: ((16 : 8) : 4) : 2
(16 : (8 : 4)) : 2 (16 : 8) : (4 : 2) 16 :((8 : 4) : 2) 16 : (8 : (4 : 2))
 Исправи грешке¶
Исправи грешке¶
Грешка 1¶
- Питање
Ученик је желео да повеже све скрипте за вођење лика кроз лавиринт у једну заједничку. Ово је његов програм који, нажалост не ради како је желео. У чему је грешка?
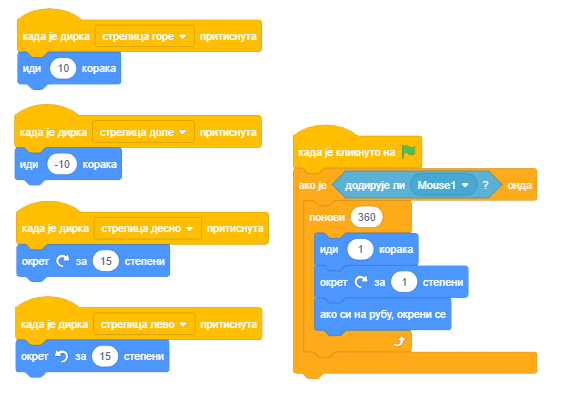
Одговор:
И лева и десна стрелица усмеравају лик удесно (90). Лева стрелица треба да усмерава кретање лика улево (-90).
Грешка 2¶
- Питање
Ученик је желео да направи једноставнију верзију пројекта лавиринт без променљивих, па је у случају додира зида лавиринта (црне боје) миша враћао на полазну позицију (23,-158). Међутим, миш је ударо у зидове лавиринта и када то ученик није очекивао. У чему је грешка?
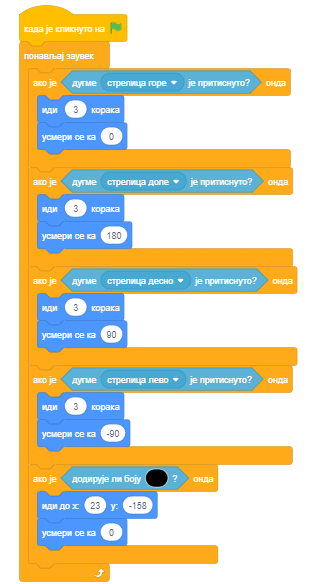
Одговор:
Лик се креће пре но што се усмери где треба, па прави кораке у смеру који је постављен претходно извршеном наредбом усмеравања.
Грешка 3¶
- Питање
И овај програм требало је да враћа миша на почетак увек када би дотако зидове лавиринта. Међутим, то се некад дешавало, а некада није. У чему је грешка?
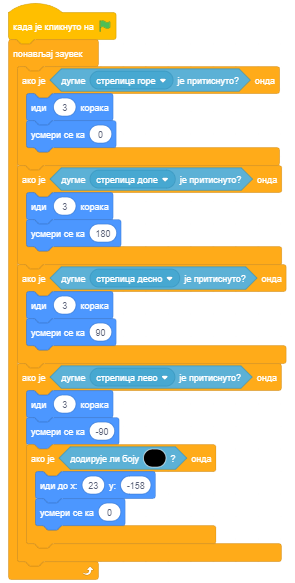
- showtitle
Прикажи одговор
- hidetitle
Сакриј одговор
Одговор:
Блок ако онда унутар кога се проверава да ли лик додирује лавиринт налази се унутар блока који проверава да ли је притиснута стрелица лево, а треба да се налази иза њега. Овако се услов додира проверава једино ако лик иде улево.
Грешка 4¶
- Питање
И овај програм требало је да враћа миша на почетак увек када би дотакао зидове лавиринта. Међутим,то се никад није дешавало. У чему је грешка?
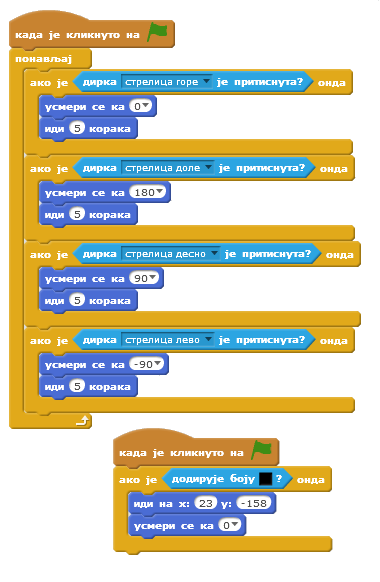
Одговор:
Да би се провера да ли лик додирује зидове лавиринта вршио стално мора да се нлази у оквиру блока понављај. Овако ће се провера извршити само једанпут.
 Шта смо научили¶
Шта смо научили¶
Појмови: израз - аритметички, логички; променљива - проста, сложена, локална, глобална.
Наредбе:  -
-  ,
,  ,
,  ,
,  .
.
Функцијски блокови:  -
-  ,
,  ,
,  ,
,  ,
,  ,
, 
 Уради неки од следећих пројеката¶
Уради неки од следећих пројеката¶
Пројекат 1 - Калкулатор¶
Започни нови пројекат који ћеш назвати Калкулатор, у којем ћеш направити калкулатор за 4 основне рачунске радње – сабирање, одузимање, множење и дељење. За ову вежбу биће вам потребни следећи ликови: Дугме са знаком +, Дугме са знаком -, Дугме са знаком * и Дугме са знаком /.
Осим тога, у апликацији ће ти бити потребне и следеће променљиве: улазне вредности x и y и Резултат.
Пројекат формирај на следећи начин:
За позадину нацртај правоугаоник у чијем горњем левом углу пише: „КАЛКУЛАТОР“
Направи све потребне променљиве и распореди их на калкулатор.
Убаци ликове за 4 дугмета помоћу којих ћеш извршавати рачунске операције и распореди их на калкулатор.
За свако од дугмади направи следећу скрипту: када се на дугме кликне мишем извршава се одговарајућа рачунска операција.
Тестирај резултат.
Калкулатор вероватно добро ради, али није очигледно која операција је последња извршена.
Зато промени калкулатор, тако да дугме које је последње притиснуто промени боју у црвено (што ће бити знак да је резултат који видимо резултат управо те операције).
Упутство: Мораш направити још по један костим за свако дугме. Нека дугме у новом костиму буде црвено. Када се кликне на дугме, скрипта би требало да пошаље поруку „Нова операција“, а затим да промени костим у црвени. Осим тога, свако дугме мора да има и једну скрипту која ослушкује поруке и када прими поруку „Нова операција“, да промени свој костим у првобитни костим.
Пројекат 2 - Програм на основу блок дијаграма¶
Направи програм у Скречу који одговара следећем алгоритму.
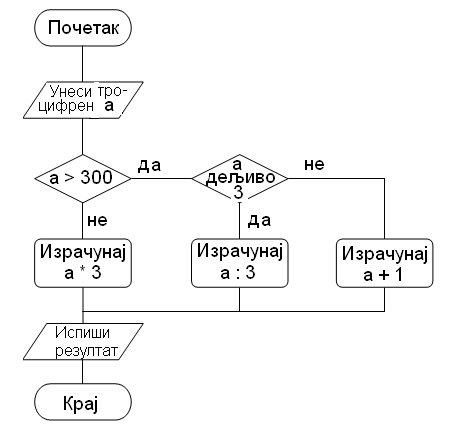
Одреди резултат извршавања тог програма за а = 157; а = 342; а = 529.
Колико цифара ће имати резултат који се добије извршавањем задатог програма?
Да ли број цифара резултата зависи од улазне вредности троцифреног броја а?
Измени дати програм тако да се као резултат увек добија двоцифрен број.
Пројекат 3 - Трка аутомобила¶
Започни нови пројекат који ћеш назвати „Трка аутомобила“, у којем ћеш направити игрицу за два играча. На позорници треба да буду 3 лика: 2 аутомобила и капија на којој пише „Циљ“. Сваки аутомобил може да се креће напред-назад и да ротира у смеру казаљке на сату и у смеру супротном казаљки на сату.
Управљачки тастери за први аутомобил су:
Стрелица на горе - Ауто иде право напред
Стрелица на доле - Ауто иде право назад
Стрелица лево - Ауто ротира у смеру супротном казаљки на сату
Стрелица десно - Ауто ротира у смеру казаљке на сату
Управљачки тастери за други аутомобил су:
Тастер W Ауто иде право напред
Тастер S Ауто иде право назад
Тастер А Ауто ротира у смеру супротном казаљки на сату
Тастер D Ауто ротира у смеру казаљке на сату
Пошто направиш скрипте за први аутомобил, клонирај га и направи неопходне измене у називима тастера и изгледу самог аутомобила. Циљна капија се појављује на позорници на случајно изабраној локацији. Аутомобили уз помоћ управљачких тастера возе до циља. Ко први додирне циљ добија 1 поен. Када ауто додирне циљ, капија нестаје са позорнице и појављује се на новој случајно изабраној локацији (води рачуна о димензијама позорнице и координатама доње-леве и горње-десне тачке). Аутомобили сада возе према новом циљу. Ко први додирне капију добија 1 поен. Капија опет нестаје и појављује се на новој локацији…. И тако у круг. Аутомобил који први сакупи 30 поена је победник. Трка се зауставља и на Позорници се исписује порука: „Победник је Играч 1“ или „Победник је Играч 2“. Да би се пратили поени сваког аутомобила, потребно је увести променљиве Играч1 и Играч2. За праћење координата циљне капије, уведи променљиве кx и кy.
Пројекат 4 - Надоградња игре Понг¶
Измени проејкат Pong тако што ћеш у игру додати променљиве.
Како се помоћу променљивих игра може начинити занимљивијом?
променљива може да регулише брзину кретања лоптице.
променљива може да мери време игре до момента промашаја лоптице.
променљива може да броји поене за сваку успешно одбијену лоптицу.
…
Креирај локалну променљиву брзина за лик ball.
Прикажи на сцени монитор променљиве са клизачем. Сада играч може да регулише брзину лоптице.
Замени у блоковима за премештање лоптице константу променљивом брзина.
Креирај локалну променљиву поени, која ће памтити број одбијања лоптице и прикажите њен монитор на сцени.
Додај скрипту која дефинише понашање лоптице после додира са рекетом. Шта ће се променити ако се у овој скрипти после заглавља не постави блок доделе вредности 0 променљивој?
Креирај још две променљиве:
старт за чување вредности тајмера од тренутка почетка игре;
време за чување дужине трајања игре као разлике између вредности тајмера у тренутку промашаја лоптице и његове почетне вредности која се чува у променљивој старт.
Додај скрипту, која треба да заустави игру.
Сачувај овај ремикс пројекта под новим именом МојPong.