Često ćete funkcije koristiti da grupišete naredbe koje rade nešto zajedno. Na primer, pogledajmo ponovo robota koji ide po pločicama. Robotu možemo da damo specijalne naredbe koje u sebi imaju druge naredbe. Kada god robot naiđe na neku specijalnu naredbu, on će znati da je ona samo ime za neku grupu naredbi i znaće da treba da izvrši njih.
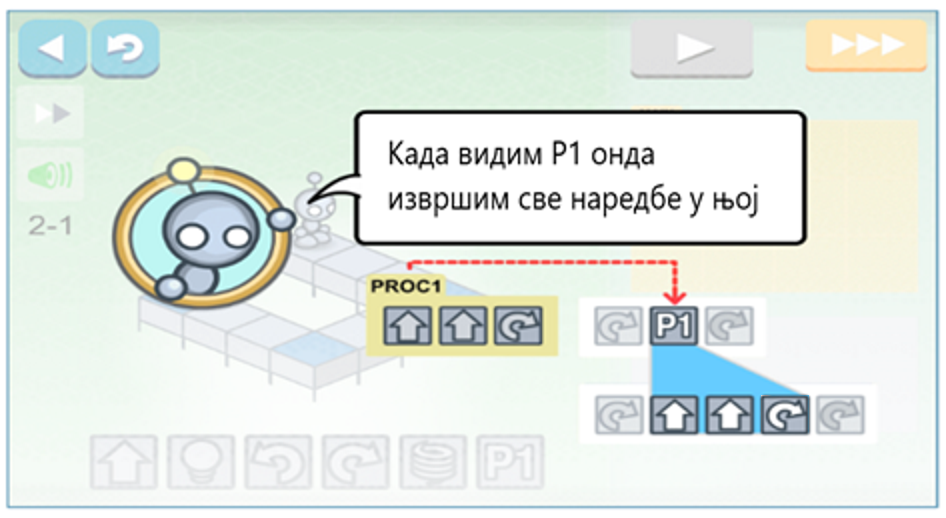
Iako imamo funkcije idi_napred() i okreni_se_ulevo(), bilo bi nam korisno da imamo i funkciju koja će odjednom da pomeri robota dva puta napred i okrene ga ulevo. Mi možemo da napravimo nove funkcije kombinujući postojeće. Na sledećoj slici je prikazan šablon koji se koristi kada se prave nove funkcije:
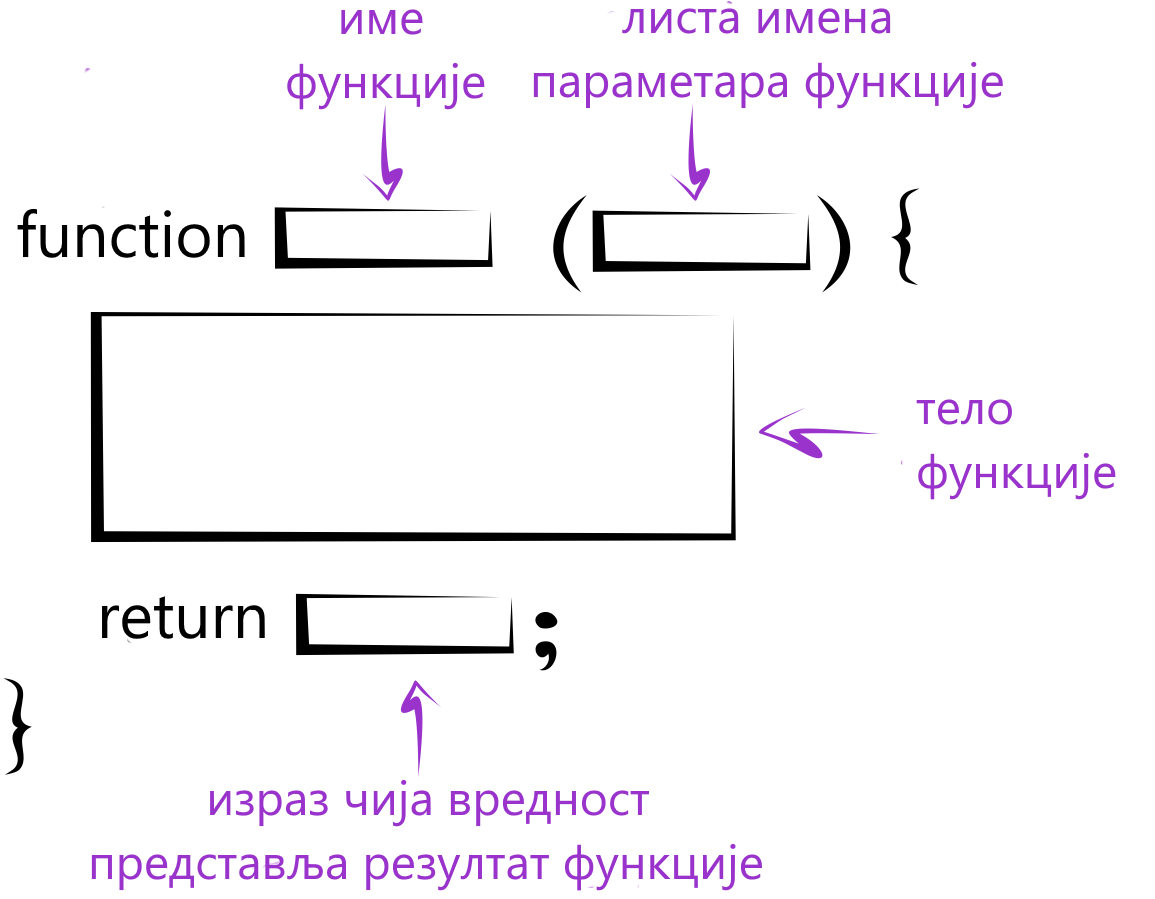
Na ovaj način se pravi nova funkcija sa datim imenom i naredbama u njenom telu koje će se izvršiti ako se u programu naiđe na ima funccije. Kada neko bude hteo da izvrši naredbe u ovoj funkciji, staviće u program ime ove funkcije sa zagradama. U zagrade možemo da stavimo imena parametara koji će biti poslati funkciji kada se funkcija pozove. Na primer, ako napravimo funkciju koja proverava da li je broj paran ili neparan, ulazni podatak koji se predaje toj funkciji je upravo broj koji treba proveriti. Ako bi trebalo da napravimo funkciju koja nalazi najmanju od vrednosti koje su joj poslate, ulazni parametri su brojevi za koje bi trebalo naći minimum.
U telu funkcije se stavljaju naredbe koje nešto rade. Konačno, ako funkcija treba da vrati neki rezultat može se napisati return neki izraz.
Kada se napravi funkcija, ona može da bude pozvana tako što se navede njeno ime i u zagradi se navedu vrednosti ili promenljive koje joj se predaju kao parametri. Kada se pozove funkcija, parametri će biti kopirani kao parametri funkcije i počeće izvršavanje naredbi koje se nalaze u toj funkciji.
Na primer, možemo da napišemo funkciju koja dobija dužine stranica pravougaonika i računa njegovu površinu i obim:
function povrsinaPravougaonika(a, b) {
return a*b
}
function obimPravougaonika(a, b) {
return 2*a + 2*b
}
Ove funkcije nam pomažu da lako rešimo matematičke zadatke kao na primer: "Dat je pravougaonik sa dužinama stranica 2 i 5. Potrebno je izračunati obim i površinu tog pravougaonika." Kada smo napisali ove funkcije, lako nam je da rešimo ovakav zadatak tako što samo stavimo date dužine stranica u funkcije za računanje površine i obima:
p = povrsinaPravougaonika(2, 5)
obim = obimPravougaonika(2, 5)
alert("Povrsina pravougnika je: " + p + ", a obim je: " + obim)
Sa ovakvim programom možemo da rešimo bilo koji zadatak ove vrste. Koje god da su dužine stranica dovoljno je samo upisati ih umesto brojeva 2 i 5.
Ali šta da radimo ako imamo dužine stranica zadate u mernim jedinicama kao što su metri, decimetri i centimetri, na primer 2m 3dm? Morali bismo prvo da pretvorimo ove dužine u decimetre ili centimetre a onda ove dobijene brojeve da prosledimo funkcijama za računanje površine i obima. Umesto da mi preračunavamo dužine, možemo da napišemo novu funkciju koja dobija dužinu u metrima, decimetrima i centimetrima (na primer 2m 3dm 8cm ) i pretvara je u dužinu u centimetrima.
function centimetri(metri, decimetri, centimetri) {
return 100*metri + 10*decimetri + centimetri
}
Sad možemo da rešavamo i zadatke kao što su: "Dat je pravougaonik sa dužinama stranica 2m 4dm 7cm i 1m 5dm 1cm. Potrebno je izračunati obim i površinu tog pravougaonika." Dovoljno je da prvo pretvorimo dužine stranica u centimetre, a onda da te dužine pošaljemo funkcijama koje računaju površinu i obim pravougaonika:
a = centimetri(2,4,7)
b = centimetri(1,5,2)
p = povrsinaPravougaonika(a,b)
obim = obimPravougaonika(a,b)
alert("Povrsina pravougnika je: " + p + ", a obim je: " + obim)
Da smo imali na primer dužine stranica 3dm 2cm i 4m 7dm, napisali bismo:
a = centimetri(0,3,2) b = centimetri(4,7,0)
Dakle, ako je neka jedinica mere izostavljena, na mesto odgovarajućeg parametra stavljamo nulu (3dm 2cm je 0m 3dm 2cm).
Kao što vidite, kad god imate neku korisnu formulu ili način da se nešto izračuna a ponavljaćete ga često, bilo bi dobro da od toga napravite funkciju i da je onda samo upotrebite gde vam treba umesto svaki put da tražite kako se nešto izračunava i da ponovo pišete deo programa koji to radi.
Primer
Izračunajte površinu pravouganika koji ima sledeće dužine stranica:
- 35dm 5cm i 3dm 5cm
- 5dm 5cm i 3.4 dm
- 5dm 5cm i 3m 5dm
- 5dm i 3m 5cm
- 3.5dm i 7.5 dm
Ako napišemo funkciju koja pretvara sve jedinice mere u centimetre, onda bi program izgledao ovako:
function cm(metri, decimetri, centimetri) {
return 100*metri + 10*decimetri + centimetri
}
alert('Provršina pravougaonika stranica 35dm 5cm i 3dm 5cm je: ' + cm(0,35,5) * cm(0,3,5) )
alert('Provršina pravougaonika stranica 5dm 5cm i 3.4 dm je: ' + cm(0,5,5) * cm(0,3.4,0) )
alert('Provršina pravougaonika stranica 5dm 5cm i 3m 5dm je: ' + cm(0,5,5) * cm(3,5,0) )
alert('Provršina pravougaonika stranica 5dm i 3m 5cm je: ' + cm(0,5,0) * cm(3,0,5) )
alert('Provršina pravougaonika stranica 3.5dm i 7.5 dm je: ' + cm(0,3.5,0) * cm(0,7.5,0) )
Kada jednom napravite funkciju koja pretvara metre i decimetre u centimetre, lako možete da ih pretvorite u centimetre i izračunate rezultat. Bez obzira koliko imate zadataka i parova stranica, dovoljno je da samo dodate još jedan red koji će pretvoriti veličine u centimetre i prikazati rezultat.
Da je zadatak bio da se pronađu obimi pravougaonika datih stranica, program bi bio veoma sličan:
function cm(metri, decimetri, centimetri) {
return 100*metri + 10*decimetri + centimetri
}
alert('Obim pravougaonika stranica 35dm 5cm i 3dm 5cm je: ' + 2*(cm(0,35,5) + cm(0,3,5)) )
alert('Obim pravougaonika stranica 5dm 5cm i 3.4 dm je: ' + 2*(cm(0,5,5) + cm(0,3.4,0)) )
alert('Obim pravougaonika stranica 5dm 5cm i 3m 5dm je: ' + 2*(cm(0,5,5) + cm(3,5,0)) )
alert('Obim pravougaonika stranica 5dm i 3m 5cm je: ' + 2*(cm(0,5,0) + cm(3,0,5)) )
alert('Obim pravougaonika stranica 3.5dm i 7.5 dm je: ' + 2 *(cm(0,3.5,0) + cm(0,7.5,0)) )
Primer
Izračunajte hipotenuzu pravouglog trougla ako su katete:
- 35 i 32 centimetra
- 15 i 9 centimetra
- 16 i 3 centimetra
- 11 i 26 centimetra
- 31 i 5 centimetra
Hipotenuza trougla se računa po Pitagorinoj teoremi:
hipotenyza = KOREN( a*a + b*b )
Nije baš jednostavno naći kvadratni koren nekog broja. Srećom, postoji funkcija
Math.sqrtkoja će izračunati koren broja i vratiti rezultat.
Pošto moramo da odredimo hipotenuzu za nekoliko parova kateta bolje bi bilo da napravimo funkciju koja određuje hipotenuzu po ovoj formuli kojoj bismo prosledili katete kao parametre. Program koji proverava da li je nejednakost trougla zadovoljena za ove duži je prikazan u sledećem primeru:
function hipotenuza(a, b) {
return Math.sqrt( a*a + b*b )
}
alert('Hipotenuza trougla sa katetama 35 i 32 je: ' + hipotenuza(35,32) )
alert('Hipotenuza trougla sa katetama 15 i 9 je: ' + hipotenuza(15,9) )
alert('Hipotenuza trougla sa katetama 16 i 3 je: ' + hipotenuza(16,3) )
alert('Hipotenuza trougla sa katetama 11 i 26 je: ' + hipotenuza(11,26) )
alert('Hipotenuza trougla sa katetama 31 i 5 je: ' + hipotenuza(31,5) )
Primer
Koje od datih duži se mogu iskoristiti da se napravi trougao:
- 29, 35 i 32 centimetra
- 25, 15 i 9 centimetra
- 18, 16 i 3 centimetra
- 14, 11 i 26 centimetra
- 25, 31 i 5 centimetra
Trougao se može napraviti od duži ako zadovoljavaju nejednakost trougla: a < b + c I b < c + a I c < b + a. Pošto moramo da odredimo da li je ovaj uslov tačan za veliki broj duži, bolje bi bilo da napravimo funkciju koja proverava da li se od ovih duži može napraviti trougao. Program koji proverava da li je nejednakost trougla zadovoljena za ove duži je prikazan u sledećem primeru:
function trougao(a, b, c) {
return ( a < b + c && b < c + a && c < b + a )
}
alert('Od duži dužina 29, 35 i 32 centimetra, se može napraviti trougao:' + trougao(29,35,32) )
alert('Od duži dužina 25, 15 i 9 centimetra, se može napraviti trougao:' + trougao(25,15,9) )
alert('Od duži dužina 18, 16 i 3 centimetra, se može napraviti trougao:' + trougao(18,16,3) )
alert('Od duži dužina 14, 11 i 26 centimetra, se može napraviti trougao:' + trougao(14,11,26) )
alert('Od duži dužina 25, 31 i 5 centimetra, se može napraviti trougao:' + trougao(25,31,5) )
Ako dobijete poruku
Od duži dužina 29, 35 i 32 centimetra, se može napraviti trougao:true to
znači da se od datih dužina može napraviti trougao, u suprotnom ako je poruka:
Od duži dužina 29, 35 i 32 centimetra, se može napraviti trougao:false, od
njih se ne može napraviti trougao.
