U prethodnoj lekciji smo se upoznali sa nizovima. Videli smo da su to složene promenljive, koje u sebi sadrže više jednostavnijih promenljivih, kojima se može pristupati po indeksu. Drugi tip složenih promenljivih su „objekti“, koji se mogu zamisliti kao skupovi promenljivih kojima se može pristupati po imenu. Kao što smo u prethodnom primeru mogli da zamislimo niz kao grupu kutija gde je svaka obeležena brojem, objekte možemo zamisliti kao grupe kutija gde je svaka obeležena nekim nazivom. Zamislite da nam treba promenljiva u koju bismo stavili podatke o nekom učeniku, kao što su njegovo ime, koliko ima godina, koji mu je broj telefona, imejl, Fejsbuk nalog, u koji razred i školu ide i u kom gradu. Umesto da stavimo osam posebnih promenljivih za ove podatke, mogli bismo da ih grupišemo zajedno i stavimo na jedno mesto. Tako možemo da stavimo iste podatke za više različitih učenika:
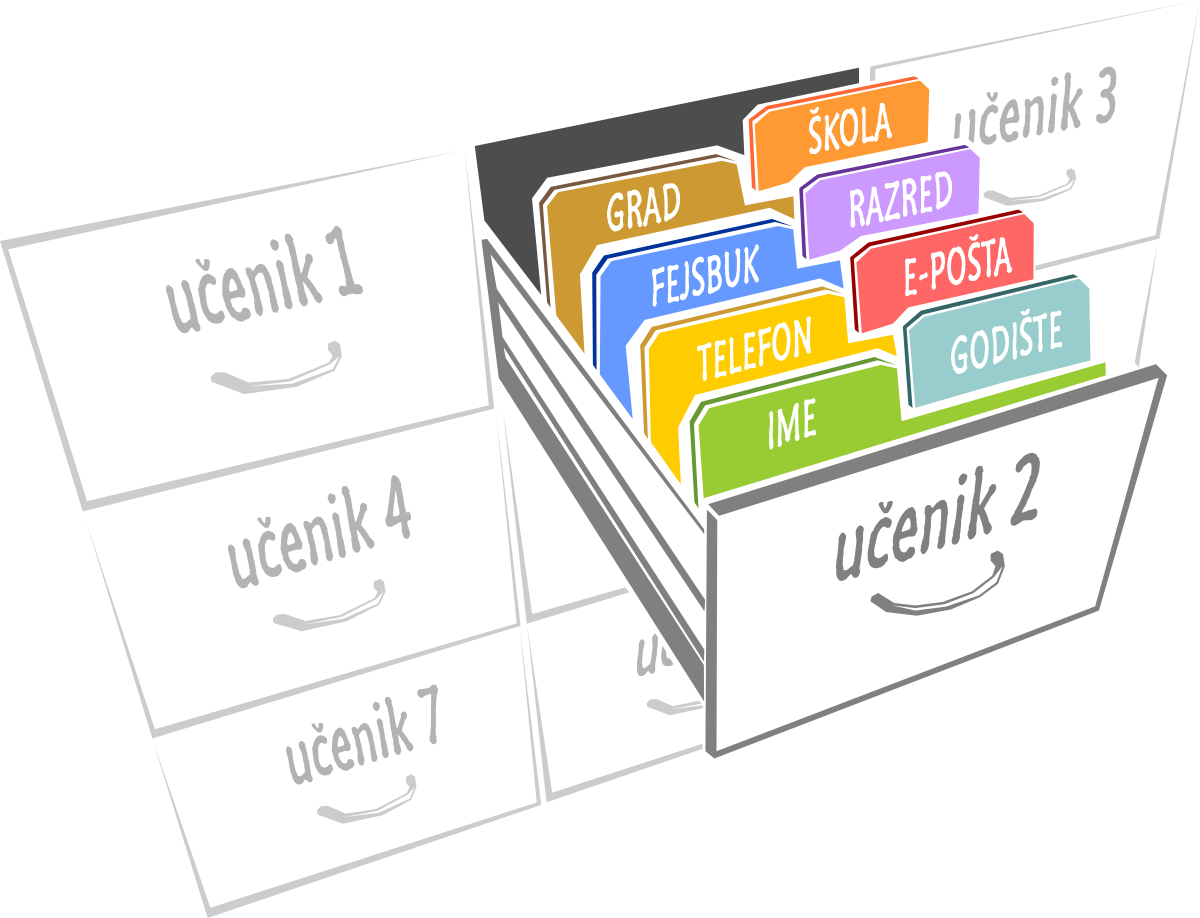
Zamislite da je svaka fioka u stvari jedna promenljiva u kojoj imamo podatke o učenicima. Kada pogledamo u podatke o nekom od učenika u njemu možemo da vidimo dodatne promenljive (fascikle) koje sadrže vrednosti kao što su u koji razred ide, koje je godište i slično.
Kao i u slučaju nizova, svaka promenljiva u objektu (koju ćemo nazivati polje objekta) sadrži neki podatak, kome možemo pristupiti nezavisno od ostalih. U JavaScript-u se ovakvi objekti prave tako što se u vitičaste zagrade stave imena polja i vrednosti koje će biti u njima:
ucenik1 = { ime: "Petar Petrović", godiste: 98, telefon: "012 345 678" }
ucenik2 = { ime: "Marko Marković", godiste: 97, telefon: "098 765 432" }
Kao rezultat napravili smo dve promenljive (osoba1 i osoba2) koje predstavljaju objekte sa dodatnim promenljivama u sebi. Imena polja moraju da budu u skladu sa pravilima imenovanja promenljivih u JavaScript-u (tj. počinju slovima, dolarom ili donjom crtom, a posle mogu da sadrže i cifre), a vrednosti mogu da budu brojevi ili stringovi.
Možete da napravite i potpuno prazan objekat ako stavite samo vitičaste zagrade bez i jednog polja, npr. x = {}. Posle možete takvom objektu da dodajete polja.
Objekti mogu da se koriste kad god imamo više podataka o jednom realnom objektu. Na primer, zamislite da imate dva ugla α=120⁰40′ i β=60⁰ 31′ 10′′. Njih možemo da predstavimo kao objekte koji imaju polja za stepene, minute i sekunde:
alfa = { stepeni: 120, minuta: 24 }
beta = { stepeni: 60, minuta: 31, sekundi: 10 }
Objekti mogu da budu i dužine duži, izražene u različitim merama kao što su metri, decimetri, centimetri i milimetri. Na primer, pomoću objekata možemo da predstavimo dve duži dužina 1m 2dm i 1dm 3cm 5mm:
duz1 = { m: 2, dm: 2 }
duz2 = { dm: 1, cm: 3, mm: 5 }
Kao što se promenljivama u nizu može pristupiti po indeksu korišćenjem uglastih zagrada (npr. imeniza[indeks]) tako se promenljivama u objektu može pristupiti po imenu polja korišćenjem tačke (npr. objekat.imePolja). U sledećem primeru možete da vidite kako se pravi objekat, kako se čita podatak iz njega i kako se upisuje vrednost u neko polje objekta.
ucenik = { ime: "Petar Petrović", tel: "012 345 678", razred: 6 }
razred = ucenik.razred
razred = razred + 1
ucenik.razred = razred
Kao i u slučaju niza, kada jednom pristupimo promenljivoj u objektu, možemo ili da čitamo njenu vrednost, ili da upišemo novu vrednost u nju. Možete i da kombinujete nizove i objekte i tako da napravite nizove objekata. Na primer zamislite da treba da u neku promenljivu stavite podatke o svim učenicima u nekom razredu. Razred će biti niz u kome će svaki element biti objekat koji ima podatke o učenicima:
razred =
[
{ ime: "Jovan Jovanović", visina: 162 },
{ ime: "Petar Petrović", visina: 167 },
{ ime: "Marko Marković", visina: 159 }
]
U ovom primeru imamo jednu promenljivu, u kojoj se nalazi niz objekata koji sadrže podatke o učenicima.
Primer - stariji učenik
U dva objekta se nalaze podaci o učenicima (ime, broj telefona, razred). Potrebno je napisati program koji pronalazi koji je od ova dva učenika stariji. Kada napravimo dva objekta, uporedićemo polja u kojima su upisani razredi. Ako je razred prvog učenika veći, on je stariji i prikazaćemo njega. U suprotnom prikazaćemo ime drugog učenika.
ucenik1 = { ime: "Petar Petrović", tel: "012 345 678", razr: 6 }
ucenik2 = { ime: "Marko Marković", tel: "098 765 432", razr: 4 }
if ( ucenik1.god > ucenik1.god ) {
alert("Učenik " + ucenik1.ime + " je stariji")
} else {
alert("Učenik " + ucenik2.ime + " je stariji")
}
Primer - najviši učenik u razredu
Razred je niz učenika u kome svaki učenik ima zapisano ime i visinu kao u primeru:
[
{ ime: "Petar Petrović", visina: 167 },
{ ime: "Marko Marković", visina: 159 }
]
Potrebno je napisati program, koji u nizu učenika pronalazi učenika koji je najviši. Prvo ćemo napraviti niz učenika u kome će biti objekti sa poljima ime i visina. Onda ćemo napraviti petlju, u kojoj ćemo jednog po jednog učenika upisati u promenljivu ucenik i u svakoj iteraciji proveriti da li je visina trenutnog učenika veća od vrednosti u promenljivoj visina. Ako jeste, to je za sada najviši učenik i njegovo ime ćemo upisati u promenljivu najvisi a njegovu visinu u promenljivu visina. Nastavićemo da prolazimo petljom kroz sve učenike u nizu i za svakog proveriti da li je viši od trenutne najveće visine.
ucenici = [
{ ime: "Jovan Jovanović", visina: 162 },
{ ime: "Petar Petrović", visina: 167 },
{ ime: "Marko Marković", visina: 159 }
]
i = 0
visina = 0
while ( i < ucenici.length ) {
ucenik = ucenici[i]
if ( ucenik.visina > visina ) {
najvisi = ucenik.ime
visina = ucenik.visina
}
i = i + 1
}
alert("Učenik " + najvisi + " je najviši")
Primer - sabiranje uglova
Potrebno je napisati funkciju koja dobija dva objekta, koji predstavljaju uglove predstavljene stepenima, minutima i sekundama (npr. α=20⁰ 10′ 45′′ i β=72⁰ 40′ 40′′) i vraća zbir ta dva ugla.
function saberi( ugao1, ugao2 ) {
zbir = {}
zbir.sek = (ugao1.sek + ugao2.sek) % 60
prenos = (ugao1.sek + ugao2.sek) / 60
zbir.min = (ugao1.min + ugao2.min + prenos) % 60
prenos = (ugao1.min + ugao2.min + prenos) / 60
zbir.stepeni = ugao1.stepeni + ugao2.stepeni + prenos
return zbir
}
Prvo ćemo da napravimo prazan objekat koji predstavlja zbir. Onda ćemo u polje tog objekta koje predstavlja sekunde da upišemo zbir sekundi iz uglova koji su poslati kao parametri. Pošto broj sekundi ne može da bude veći od 60, ali može da se desi da zbir sekundi bude veći od 60 (npr. ako sabiramo α=20⁰ 10′ 45′′ i β=72⁰ 40′ 40′′ dobićemo 85′′ sekundi), u polje objekta ćemo upisati ostatak zbira pri deljenju sa 60 (tj. %60) što je u ovom slučaju 25′′. Zašto ostatak? Zato što sve što bude preko ostatka predstavlja vrednost koja će biti preneta u minute. Pošto možda treba da prenesemo broj sekundi iz zbira koji je prešao preko 60, izračunavamo i količnik pri deljenju ovog zbira sa 60. To je vrednost u promenljivoj prenos, koju ćemo dodati minutima. Na isti način ćemo izračunati i vrednost minuta, kao zbir prenosa i minuta iz objekata sabiraka, gde opet nalazimo ostatak pri deljenju sa 60 da ne bismo upisali broj veći od 60. Zatim izračunavamo i vrednost koja će biti preneta u stepene kao količnik ovog zbira i broja 60. Na kraju, da bismo odredili stepene, potrebno je da saberemo stepene iz ovih objekata i dodamo vrednost koju smo preneli.
