Час 13 - Анимације више објеката, oчитавање миша и тастатуре¶
Анимације више објеката¶
Аутомобил и авион¶
Напиши програм који приказује анимацију авиона који се креће по
небу и аутомобила који се креће по земљи, при чему је брзина авиона
два пута већа него аутомобила. Када неко возило изађе на десном
крају екрана, појављује се поново на левом. Поново можеш употребити
слике auto.png и avion.png.


Задатак веома једноставно можемо решити тако што практично два пута поновимо кôд који смо написали у програму у ком смо вршили симулацију аутомобила. Понављање истог или сличног кода више пута је иначе веома лоша пракса и касније ћемо видети начине да се то избегне када се ради са више објеката, али с обзиром на то да се овде кôд понавља само једном, то можемо толерисати.
Две лоптице¶
Напиши програм који приказује црвену и плаву лоптицу које се крећу по екрану, одбијају од ивица и одбијају међусобно (једноставности ради претпостави да приликом сударе две лоптице једноставно размене векторе кретања).
Поново независно вршимо анимацију два различита објекта. Кључна новина је то што се објекти могу међусобно сударати. Два круга се сударају (пресецају) ако и само ако је растојање њихових центара веће од збира њихових полупречника. Растојање рачунамо на уобичајени начин, Питагорином теоремом. Ако се лоптице сударају, размењујемо им помераје по x и помераје по y оси (векторе брзине).
Пахуљице¶
Напиши програм који приказује анимацију пахуља које падају са врха
на дно екрана. Можеш употребити слику pahulja.png. Када пахуље
падну на дно екрана, нове крећу да падају са врха.

Центре пахуљица можемо памтити у листи парова. Један начин да реализујемо померање пахуљица је тај да од текуће листе направимо нову у којој ће x координате свих елемената бити неизмењене, а у којој ће y координате бити увећане за 1. При том, из листе можемо избацити пахуље које су пале испод дна екрана (којима је y координата врха већа од висине прозора) и за сваку пахуљу која испадне у листу додамо нову пахуљу (њој координате одређујемо насумично, тако да се по ширини налази унутар прозора, а да по висини креће да пада из појаса изнад екрана који је широк једну петину екрана).
Очитавање миша и тастатуре¶
Корисник интеракцију са програмом обично врши мишем или тастатуром. Напреднији облици интеракције подразумевају реаговање на догађаје и њих ћемо описати у наредном поглављу посвећеном догађајима. Ипак наше анимације можемо веома једноставно учинити интересантнијим помоћу веома једноставне функционалности очитавања стања миша и тастатуре (за шта нам нису потребни догађаји).
Функција
pg.mouse.get_pos()враћа уређени пар координата тачке на којој се тренутно налази показивач миша.Функција
pg.mouse.get_pressed()враћа торку од три елемента (уређену тројку), који се користе као логичке вредности. Елементи торке редом одговарају левом, средњем и десном тастеру миша. ВредностTrueозначава да је тастер притиснут, аFalseда није. Тако се, на пример, условомif pg.mouse.get_pressed()[0]:могу оградити наредбе које се извршавају само ако је притиснут леви тастер миша.Функција
pg.key.get_pressed()враћа торку чији се елементи користе као логичке вредности, а показују за сваки тастер на тастатури да ли је он тренутно притиснут или не. Пошто је тастера пуно, за њихово очитавање се користе именоване константе. Константеpg.K_LEFT,pg.K_RIGHT,pg.K_UP,pg.K_DOWNодговарају тастерима са стрелицама, размаку одговара константаpg.K_SPACE, док тастерима слова, на пример a, b, c, одговарају константеpg.K_a,pg.K_b,pg.K_cитд. Тако се, на пример, условомif pg.key.get_pressed()[pg.K_SPACE]:могу оградити наредбе које се извршавају само ако је притиснут тастер за размак.
У овом приручнику нећемо пуно инсистирати на коришћењу ове технике, јер ћемо детаљније обрадити механизам догађајај. Прикажимо само неколико једноставних примера.
Анимирани лептир кога померамо мишем¶
Напиши програм који приказује анимираног лептира који лети по
екрану и чији се центар налази увек тачно изнад показивача миша.
За анимацију можеш употребити слике leptir1.png и
leptir2.png.


Лоптица која прати миша¶
Напиши програм који приказује лоптицу која се увек полако креће ка тренутној позицији миша.
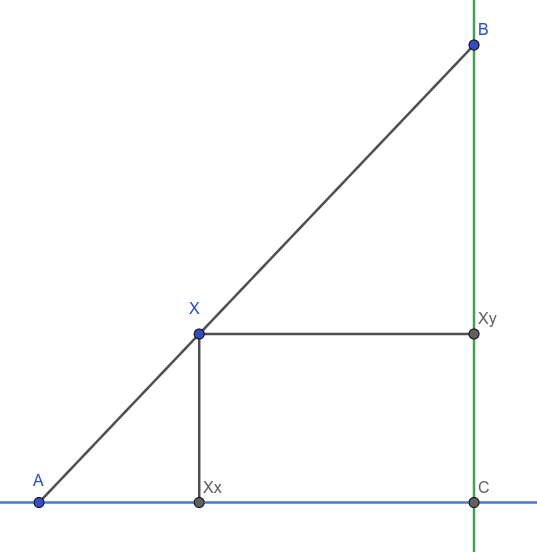
У програму ћемо памтити текућу позицију лоптице. Кључно питање је како одредити позицију лоптице у наредном фрејму. Нека тачка \(A\) представља текућу позицију центра лоптице, нека тачка \(B\) представља текућу позицију показивача миша и нека тачка \(X\) представља нову позицију центра лоптице. Пошто се центар помера из тачке \(A\) у тачку \(X\) лоптица у једном фрејму пређе пут једнак растојању између те две тачке. Обележимо ту вредност са \(v\) (ако хоћемо да се лоптица креће глатко, број фрејмова у секунди треба да буде већи, а то треба да буде нека мала вредност). Поставља се питање колико по хоризонтали и колико по вертикали треба да се помери лоптица. Троуглови \(AX_xX\) и \(ACB\) су слични. Зато се дужине \(AX_x\) и \(X_xX\) које представљају хоризонтално и вертикално померање могу израчунати на основу дужине \(AX\) која је једнака \(v\), дужине \(AB\) која се може израчунати Питагорином теоремом као растојање између тачке \(А\) и \(B\) чије су нам координате познате, дужине \(AC\) која је једнака разлици између x координата тачака \(A\) и \(B\) и дужне \(BC\) која је разлика између њихових y координата. Важи да је \(AX_x:AX = AC:AB\), као и да је \(XX_x:AX = BC:AB\) одакле се израчунавају координате непознате тачке \(X\).