Садржај
1. Робот Карел - Линијски програми и бројачка петља
2. Робот Карел - Условна петља и гранање
3. Робот Карел - Задаци за вежбање
4. Корњача графика - Линијски програми и петље
5. Корњача графика - Гранање, угнежђене петље, функције, торке и листе
6. Корњача графика - Задаци за вежбање
7. Израчунавања - Изрази, оператори, променљиве
8. Израчунавања - Цели и реални бројеви, дељење
9. Израчунавања - Коришћење и дефинисање функција
10. Израчунавања - Задаци за вежбање
11. Гранање
12. Понављање - петље
13. Контрола тока - Задаци за вежбање
14. Структуре података
15. Примена петље у структурама података
16. Откривање и исправљање грешака и коришћење дебагера
5.3. Функције¶
Да бисмо вам приближили појам функције, хајде да размишљамо на следећи начин:
Када бисмо радили неки већи посао, било би корисно да имамо помоћнике који ће нам урадити неки део посла. Функција би у програму била управо један наш помоћник! Она обично нешто израчуна за нас и врати нам резултате који су нам потребни како би наставили даље, али некада и само уради нешто нпр. нацрта неки део цртежа као што ће то бити у следећем примеру.
Функција има свој назив и своје параметре наведене у заградама који су јој потребни да би могла да изврши задатак.
Наредбе функције куцамо само на једном месту које се назива тело функције, а затим позивамо је у помоћ када год нам то затреба!
Функција за цртање испрекидане линије¶
Напишимо (дефинишимо) функцију која исцртава испрекидану линију а као параметар прослеђује јој се број цртица које желимо да линија има.
# funkcija za crtanje isprekidane linije# parametar je broj crtica ndef isprekidana_linija(n): for i in range(n): # n puta ponovi: turtle.pendown() # spusti olovku turtle.forward(20) # idi napred 20 koraka turtle.penup() # podigni olovku turtle.forward(20) # idi napred 20 koraka(функција_1)
Дефиниција функције започета је кључном речју def, након чега је наведен назив функције
(у нашем примеру, то је био isprekidana_linija), а потом параметар функције у
заградама (ако их има више раздвајају се зарезима). Након двотачке,
наведен је програмски код који чини тело функције, увучен у односу на прву линију
(слично као што је и тело наредби for, while и if увек увучено). Тело сачињавају
наредбе које се извршавају сваки пут када се функција позове.
Дефинисањем функције дефинисали смо заправо нову наредбу коју можемо користити у програму.
Нацртајмо испрекидану линију тако што ћемо користиути ту нову наредбу (позваћемо претходну функцију наводећи њен назив а као параметар проследићемо број цртица које желимо да испрекидана линија има).
import turtle# funkcija za crtanje isprekidane linije# parametar je broj crtica ndef isprekidana_linija(n): for i in range(n): # n puta ponovi: turtle.pendown() # spusti olovku turtle.forward(20) # idi napred 20 koraka turtle.penup() # podigni olovku turtle.forward(20) # idi napred 20 korakaisprekidana_linija(5) # pozivamo funkciju da iscrta isprekidanu liniju sa 5 crtica(испрекидана_линија_функција)
Функција за цртање многоугла¶
Приметимо да се цртање многоугла (каже се и полигона) јавило у више различитих програма. Стога је корисно дефинисати функцију за цртање многоугла. Параметри те функције биће број страница полигона и дужина једне странице.
# funkcija za crtanje pravilnog poligona# parametri su broj stranica poligona n i duzina stranice adef poligon(n, a): for i in range(n): # n puta ponovi: turtle.forward(a) # idi napred a koraka turtle.right(360 / n) # okreni se za spoljasnji ugao n-tostranog pravilnog poligona(функција)
Након ове дефиниције, квадрат чија је страница дужине 100
пиксела нацртаћемо тако што наведемо poligon(4, 100), а шестоугао
димензије 50 тако што наведемо poligon(6, 50). Са функцијом за
цртање многоугла на располагању, наш програм за цртање три квадрата
различите боје је доста једноставније написати и постаје доста
разумљивији.
import turtle# definisemo funkciju za crtanje pravilnog poligona# parametri su broj stranica poligona n i duzina stranice adef poligon(n, a): for i in range(n): # n puta ponovi: turtle.forward(a) # idi napred a koraka turtle.right(360 / n) # okreni se za spoljasnji ugao n-tostranog pravilnog poligonafor i in range(3): # 3 puta ponovi: poligon(4, 50) # nacrtaj kvadrat dimenzije 50 koraka turtle.right(360 / 3) # kvadrati su pravilno rasporedjeni duž punog kruga, pa se okreni za 120 stepeni(полигон_функција)
Покушај да измениш претходни програм тако да уместо квадрата црта три шестоугла дужине страница 80 пиксела.
Четири квадрата¶
Напиши програм у којем корњача црта облик који се састоји од четири квадрата, како је приказано на наредној слици.
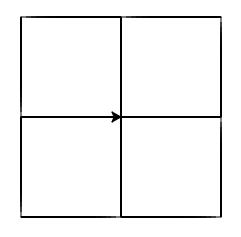
Дефиниши функцију за цртање квадрата, а затим размисли како су ти квадрати међусобно распоређени, тј. колико треба да се окрене корњача након што заврши са цртањем сваког квадрата.
import turtlen = 100# dopuni resenje(четири_квадрата)