Математика Перлиновог шума¶

Перлинов шум теоријски може да се дефинише као функција било којег броја променљивих. У претходној лекцији смо га користили као функцију једне променљиве, а сада као функцију две променљиве. Како можемо да израчунмао вредности Перлинове функције?

Да бисмо што једноставније одговорили на ово питање, потребан је мали увод.

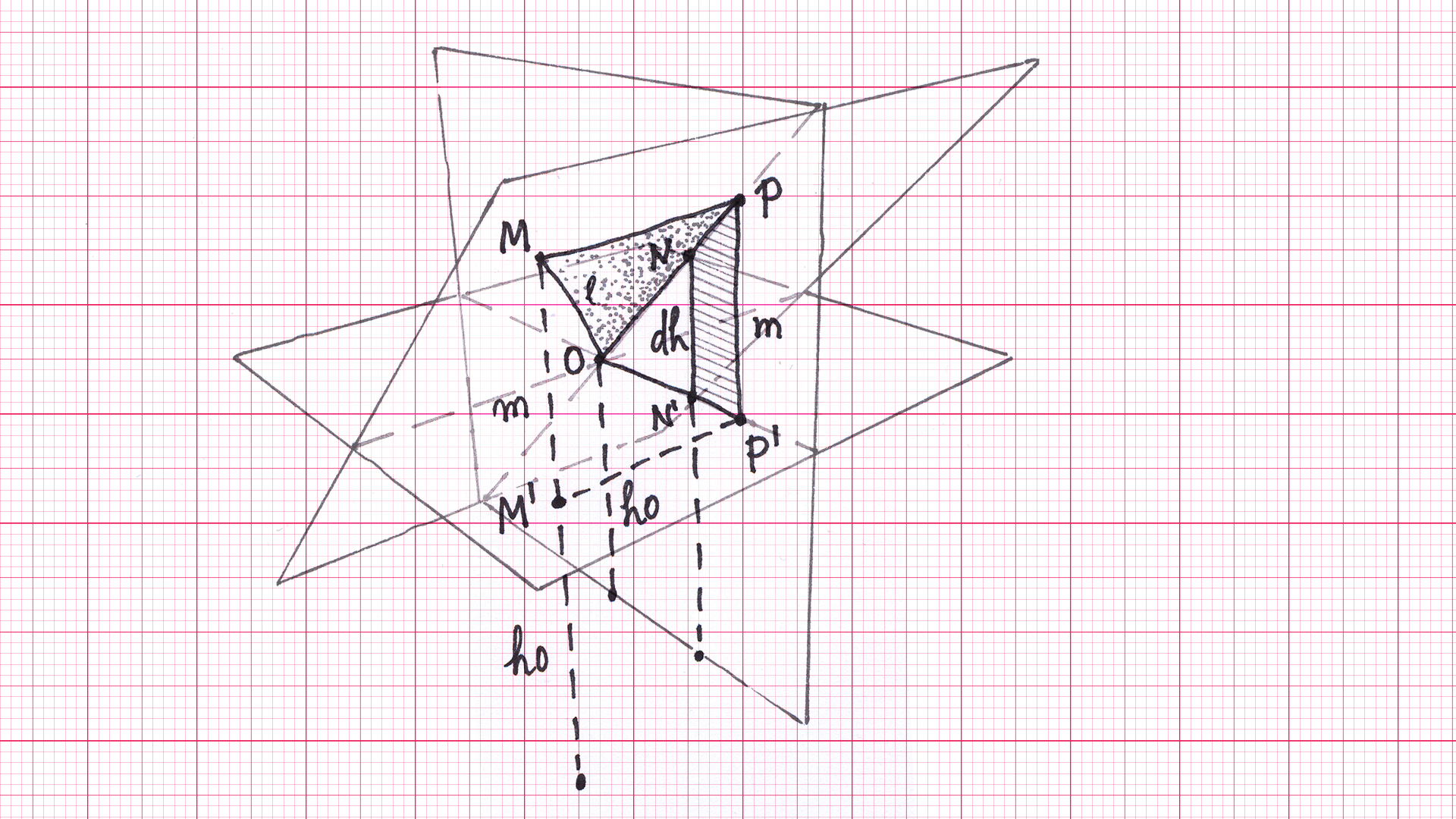
Замсли да си на равној, али стрмој ливади у тачки \((x_0, y_0)\), на висини \(h_0\) (слика 3). Црвена стрелица је јединични вектор \(\overrightarrow{v}\) смера најстрмијег успона. Нека је висинска разлика између крајева црвене стрелице једнака \(\Delta h\). Питање је како да одредимо висину у произвољној тачки \((x, y)\)?

Слика 3¶

Означимо са \(l\) растојање између тачака \((x_0, y_0)\) и \((x, y)\), а са \(\alpha\) угао између два смера означена стрелицама. Није тешко извести формулу да је висина у тачки \((x, y)\) једнака \(h = h_0 + \Delta h \cdot l \cos \alpha\). Такође, користећи адиционе формуле (конкретно, формулу за косинус разлике углова), може се извести и формула \(l \cos \alpha = (x-x_0) v_x + (y-y_0) v_y\), где су \(v_x, v_y\) дужине компоненти вектора \(\overrightarrow{v}\). Спајањем ове две формуле, коначно се добија \(h = h_0 + \Delta h \cdot ((x-x_0) v_x + (y-y_0) v_y)\).

Приметимо да висина \(h\) у тачки \((x, y)\) може да буде и једнака, па и мања од \(h_0\). Н апример, ако је угао \(\alpha\) прав, тачке \((x_0, y_0)\) и \((x, y)\) су на истој висини, а ако је угао туп, тачка \((x, y)\) је нижа од тачке \((x_0, y_0)\) тј. \(h < h_0\).

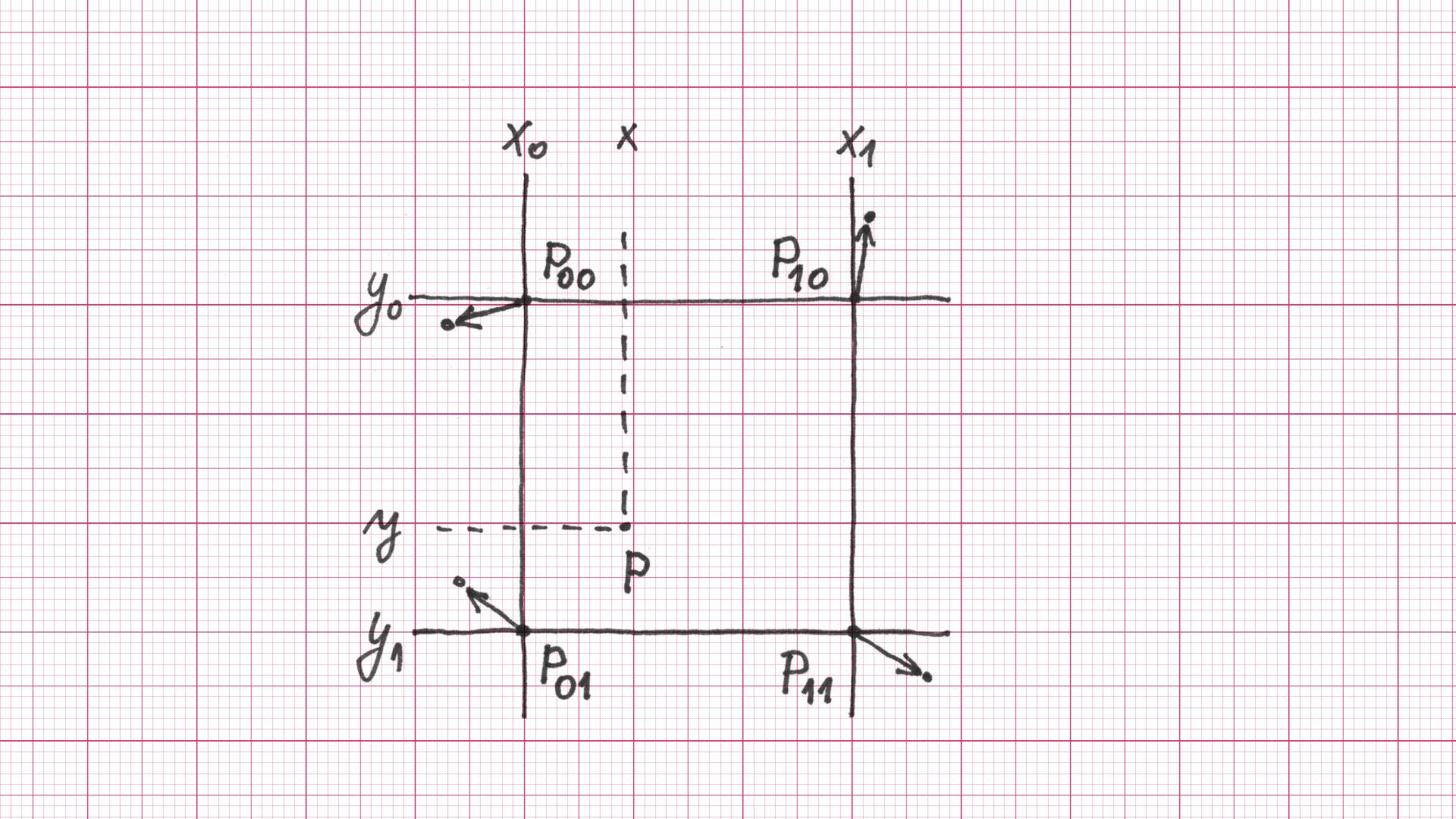
Вратимо се сада рачунању Перлинове функције. Вредности функције замишљамо као висине на неравном терену, на коме се нагиб мења потпуно неправилно. Увешћемо решетку, која се састоји од тачака \(P_{ij}\), које формирају мрежу квадрата. Терен иницијализујемо тако што у тачкама решетке насумично бирамо висине и јединичне векторе најстрмијег успона у околини тачке. Када изаберемо те почетне елементе, помоћу њих треба да дефинишено вредности функције (тј. висине) за све остале тачке, тако да се добије глатка површ. Посматрајмо произвољну тачку \(P(x, y)\) чију висину желимо да дефинишемо. Нека су \(P_{00}, P_{01}, P_{10}, P_{11}\) четири њој најближе тачке решетке, које формирају квадрат (слика 4). .

Слика 4¶

Уведимо сличне ознаке као у уводном проблему: нека је \(h_{00}\) висина у тачки \(P_{00}\), нека је \(\overrightarrow{v_{00}}\) јединични вектор најстрмијег нагиба у \(P_{00}\) (то је црвена стрелица из тачке \(P_{00}\)), нека се дуж овог вектора постиже висинска разлика \(\Delta h_{00}\), нека је \(l_{00}\) дужина дужи \(P_{00}P\) и нека је \(\alpha_{00}\) угао између вектора \(\overrightarrow{v_{00}}\) и \(\overrightarrow{P_{00}P}\). На исти начин уводимо све ове ознаке и за тачке \(P_{01}, P_{10}, P_{11}\).

Ако бисмо сада висину тачке \(P\) израчунали, на пример, само на основу тачке \(P_{01}\) (као у уводном проблему), та висина би била \(f_{01} = h_{01} + \Delta h_{01} \cdot l_{01} \cos \alpha_{01} = h_{01} + \Delta h_{01} \cdot ((x-x_0)v_{01x}+(y-y_1)v_{01y})\). Слично можемо да задамо висину тачке \(P\) и преко остале три тачке и добијемо вредности \(f_{00}, f_{10}, f_{11}\). Коначну вредност \(f\) ћемо да изразимо у облику

\(f = k_{00} \cdot f_{00} + k_{01} \cdot f_{01} + k_{10} \cdot f_{10} + k_{11} \cdot f_{11}\),

где је још потребно погодно изабрати коефицијенте \(k_{00}, k_{01}, k_{10}, k_{11}\), тако да се добије глатка површ. Да би то постигао, Перлин је изворно користио функцију \(\phi(t) = 3t^2-2t^3\) дефинисану на интервалу \([0, 1]\), а која се по потреби може додефинисати тако да је једнака нули лево, а јединици десно од интервала \([0, 1]\).

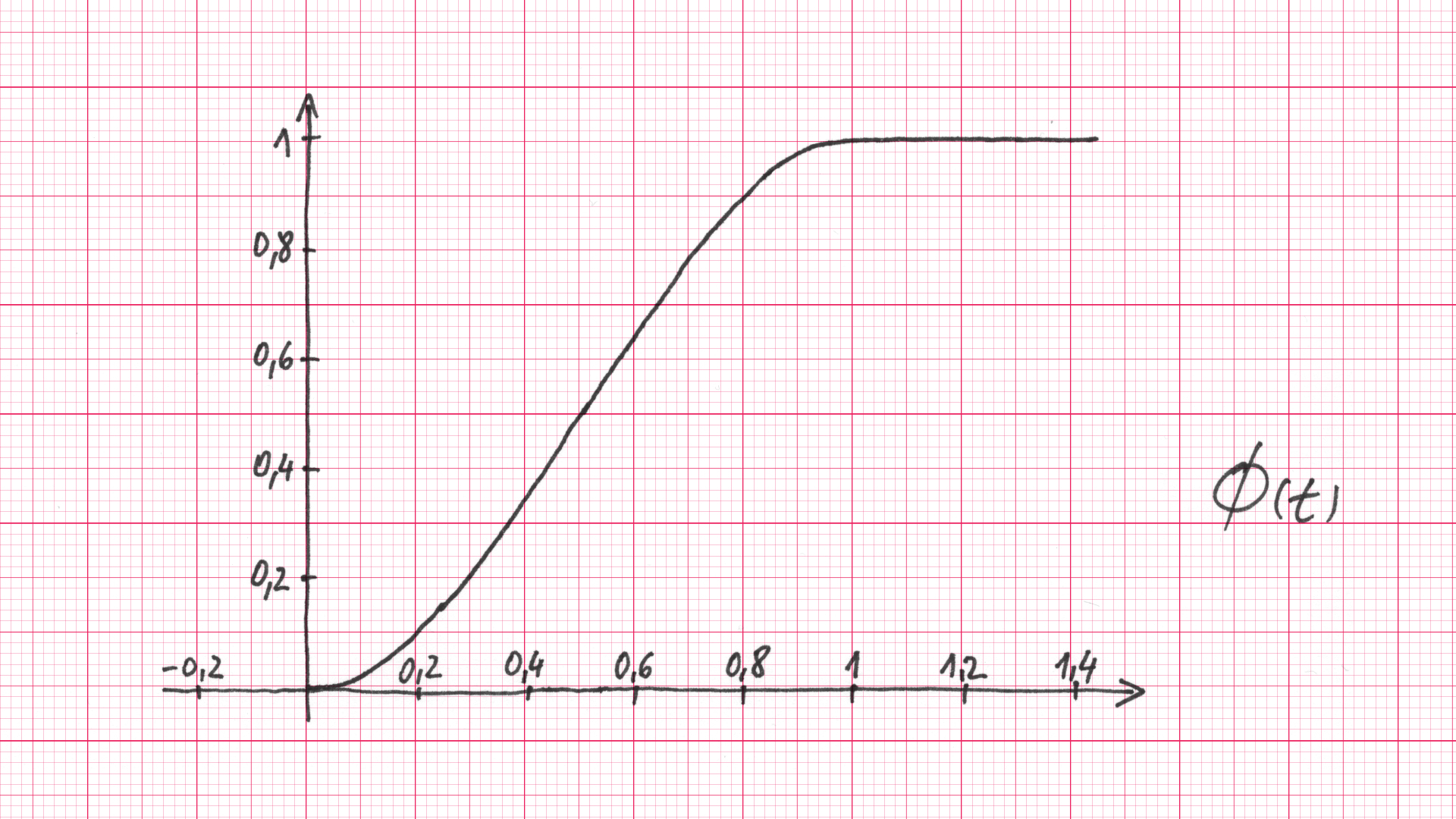
Слика 5: функција \(\phi(t)\)¶

Дефинисањем

\(\begin{align} \\ k_{00} = \phi(x_1-x) \phi(y_1-y) \\ k_{01} = \phi(x_1-x) \phi(y-y_0) \\ k_{10} = \phi(x-x_0) \phi(y_1-y) \\ k_{11} = \phi(x-x_0) \phi(y-y_0) \\ \end{align}\)

добијамо коефицијенте са свим потребним особинама. На пример, што је тачка \(P\) ближе тачки \(P_{01}\), то је коефицијент \(k_{01}\) ближи јединици и обрнуто, што је тачка \(P\) даље од тачке \(P_{01}\), то је коефицијент \(k_{01}\) ближи нули. Исто важи и за остале коефицијенте и остале тачке. Захваљујући томе, висине се глатко мењају унутар квадрата. Чак и када тачка \(P\) пређе у суседни квадрат, вредности фунцкције се глатко настављају. Перлин је заиста заслужио сва признања која је добио. Ово није само примена математике у уметности, ово је и уметност у примењивању математике!

На слици 6 је приказано како се постепено може израчунати вредност функције Перлиновог шума као фунцкције две променљиве. Висине су представљене променом боје од црвене до зелене.

Слика 6¶

На сликама у првом реду је у сваком квадрату примењена само по једна од четири функције \(f_{00}, f_{01}, f_{10}, f_{11}\). У другом реду су сабране по две од ових функција, а у трећем су сабране све четири и добијена је коначна функција перлиновог шума.