6.1.1. Проблем „златне” круне¶

Данашња прича нас води у далеку прошлост све до античке Грчке, једног чувеног града по имену Сиракуза (Сицилија, Италија) и једног генијалног научника, Архимеда.

Архимед је међу првима сматрао да математику треба и практично применити и то баш у физици.

О томе колико је овај научник био испред свог времена говоре и бројне легенде о њему. Према једној од њих, први се досетио да искористи огромна огледала и усмери сунчеву светлост у једну тачку, стварајући тако прву соларну пећ.

Открио је и закон полуге, о којем ћеш учити касније.

Ипак, данашња прича посвећена је једном чувеном купању.

Краљ Хијерон је желео да има круну од чистог злата и наручио је да му се направи таква. Али када је круна стигла краљ је почео да се пита да ли је заиста од чистог злата или има и сребра у њој. У то време није постојао начин да се ово утврди сем да се круна истопи, али то би је уништило, а краљ није желео тако нешто. Сребро је тада било далеко јефтиније од злата и често су се у златне предмете убацивали и делови сребра не само због цене, већ и да би предмет био чвршћи. Краљ је позвао Архимеда и замолио га да осмисли начин на који ће утврдити има ли сребра у његовој круни. Архимед је прихватио изазов, али решење није било лако пронаћи.

Архимед се трудио и трудио, али решење му је стално измицало. Незадовољан и разочаран, Архимед је одлучио да се мало опусти и оде на купање у топлој води. Напунио је каду до врха, ушао у њу и приметио да је вода исцурела са стране, а да његово тело плута у води. Не часећи ни часа, Архимед је истрчао из купатила и отрчао до своје куће вичући: „ЕУРЕКА, ЕУРЕКА“, чувене речи које и данас користимо, а које значе ПРОНАШАО САМ!!!

А шта је то открио Архимед, сада ћемо објаснити.

Погледај следећу симулацију. На њој смо представили једно буре. Ово буре може да плута у различитим течностима (алкохол, уље, вода и жива). Твој задатак је да погледаш ову симулацију, покренеш је и видиш шта се дешава за различите масе које смо убацили у буре.

На основу симулације одговори на следећа питања?

6.1.2. Хидростатички притисак¶

Да бисмо објаснили шта се заправо дешава, мораћемо да се присетимо лекције из шестог разреда о хидростатичком притиску.

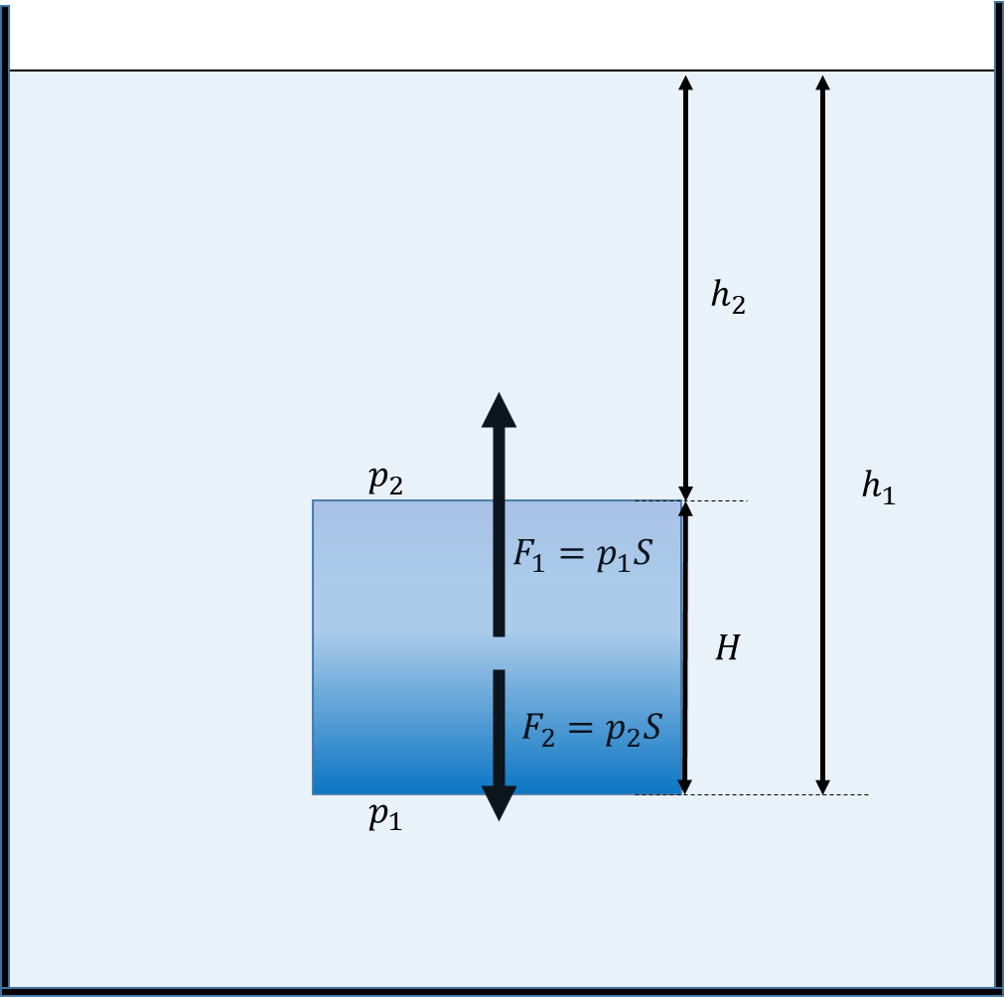
Када ронимо, течност изнад нас делује неком тежином и ми то осећамо као хидростатички притисак. Овај притисак расте са дубином, а зависи и од густине течности. Можемо га израчунати према следећој једначини:

где је \(p\) хидростатички притисак, \(ρ_0\) густина течности, \(g\) убрзање земљине теже и \(h\) дубина на којој се тело налази.

Хидростатички притисак

Човек је навикнут да живи на атмосферском притиску (око 100,000 Pa). Са повећањем дубине повећава се и притисак који делује на нас (хидростатички и атмосферски делују заједно) и већ на дубини од 10 метара притисак је два пута већи од атмосферског. Овако велики притисак, током дужег периода, може бити веома опасан по здравље. Светски рекорд у роњену без опреме (слободно роњење) износи невероватних 214 метара. Али, за овако нешто потребне су године вежбања.

Рониоци који морају да остану дуже времена на великим дубинама, обавезно користе опрему попут ове на слици изнад, како би заштитли себе од бројних последица.

Напоменимо још и да постоје рибе које живе на великим дубинама и које не би поднеле да их изнесемо на површину. Оне су навикле на огромне притиске који владају на великим дубинама.

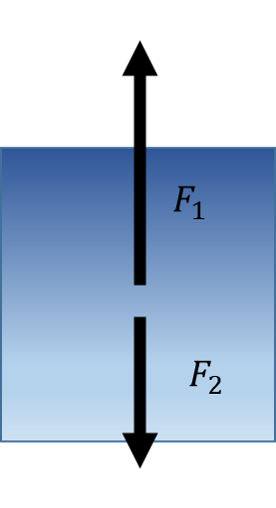
Ако посматрамо тело које је уроњено у течност, можемо видети да хидростатички притисак није једнак са горње и доње стране тела. Са бочних страна ови притисци јесу једнаки (и расту са дубином) па се укупна сила која делује на тело са стране може поништити. Овде смо, ради илустрације, деловање притиска приказали стрелицама. Стрелице представљју силе којима хидростатички притисак делује на тело.

Шта мислите, са које стране делује већи притисак?

Погледајмо сада како делују силе настале усред хидростатичког притиска. Подсетимо се само да силу можемо да израчунамо као производ притиска и површине на коју он делује \(F=p \cdot S\)

Овде смо силу којом хидростатички притисак делује на доњу површину тела обележили са \(F_1\), док смо силу којом хидростатички притисак делује на горњу површину обележили са \(F_2\). Ако се сетиш лекције о слагању сила, видећеш да је у овом случају резултујућа сила усмерена навише.

Уз мало труда и рачунања, силу потиска можемо да изразимо на још један начин, који је знатно кориснији у практичном раду.

Ако те интересује како долазимо до ове формуле за силу потиска, кликни на дугме испод.

Израчунавање силе потиска

Драго нам је да желиш да научиш више. Овде ћеш видети како долазимо до формуле за силу потиска.

Пођимо најпре од онога што смо научили у лекцији о слагању сила. Када две силе делују на тело у истом правцу а супротним смеровима, њихова резултанта ће имати смер јаче силе, док ће њен интезитет бити једнак разлици ових сила. Ради једноставности, посматраћемо тело облика квадра, површине основе \(S\), уроњено у течност густине \(ρ_0\). Пођимо од прве формуле за силу потиска:

\[F_p = F_1 - F_2\]

Погледајмо слику тела уроњеног уводу, на којој су обележене висине:

можемо да одредимо хидростатичке притиске \(p_1\) и \(p_2\)

\[ \begin{align}\begin{aligned}p_1 = ρ_0 g h_1\\p_2 = ρ_0 g h_2\end{aligned}\end{align} \]

а затим и силе којима хидростатички притисак делује на тело са горње и доње стране:

\[ \begin{align}\begin{aligned}F_1 = p_1 \cdot S = ρ_0 g h_1 S\\F_2 = p_2 \cdot S = ρ_0 g h_2 S\end{aligned}\end{align} \]

Сада можемо да израчунамо и силу потиска као разлику ове две силе:

\[F_p = F_1 - F_2 = ρ_0 g h_1 S - ρ_0 g h_2 S = ρ_0 g S (h_1-h_2)\]

Приметимо још нешто. Израз у загради је разлика дубина врха и дна тела које посматрамо што је заправо висина тела \(h_1-h_2 = H\)

Сада наш израз са силу потиска постаје:

\[F_p=ρ_0 g S H\]

У овом изразу се појављује \(S H\), што је у ствари запремина тела које је уроњено у течност, \(V\). Сада имамо коначан израз са силу потиска:

\[F_p=ρ_0 g V\]

Пре него што наставимо, напоменућемо још једном да у формули за силу потиска узимамо запремину само оног дела тела који је испод површине течности.

Погледајмо случај као на слици:

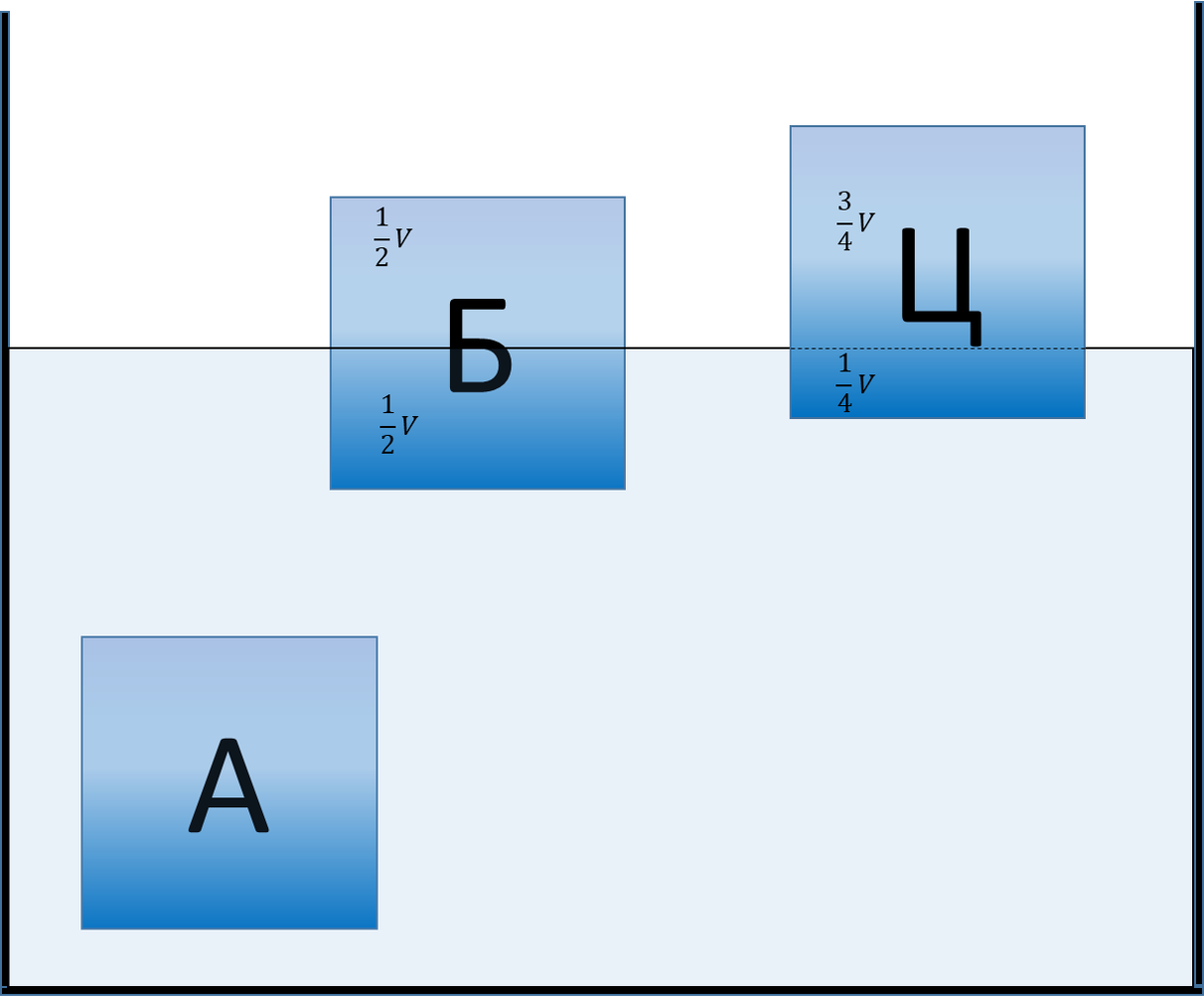
За тело А ћемо узети целу запремину, за тело Б половину запремине, а за тело Ц само четвртину.

Пробај да одговориш на следећа питања:

6.1.3. Плива или тоне¶

Хајде сада да погледамо које све силе делују на тело уроњено у течност. Поред силе потиска \(F_p\), ту је и сила теже \(mg\).

Од односа ових сила зависиће да ли ће тело потонути, плутати или испливати на површину течности.

Зашто је то тако?

Пре свега, ове силе делују увек у супротним смеровима. Сила теже покушaва да натера тело да „падне” док сила потиска покушава да га избаци из течности. Право питање је - ко је ту јачи?

Посматрајмо три случаја:

Сила теже је јача

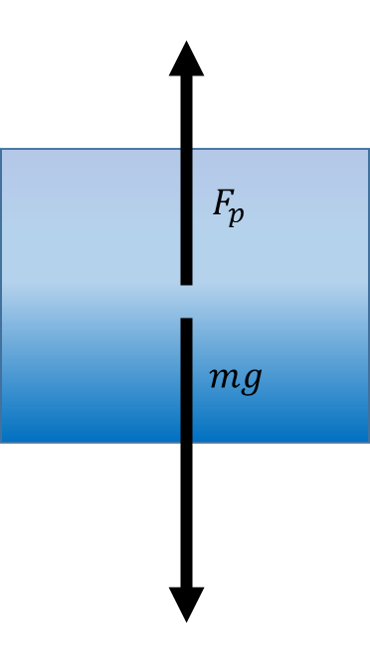
Резултујућа сила у овом случају има исти смер као и сила теже. Овo значи да ће тело потонути.

Сила потиска је јача

У овом случају резултујућа сила има исти правац и смер као и сила потиска. Ово тело неће потонути.

Сила потиска и сила теже су једнаке

У овом случају резултујућа сила је једнака нули и ово тело може да стоји непомично у течности.

Рибе користе управо овај принцип како би се попеле или спустиле до веће дубине. Помоћу рибљег мехура, оне могу да промене своју запремину и тиме повећају или смање силу потиска. Из формуле \(F_p=ρ_0 g V\) може да се закључи да већа запремина значи и већу силу потиска.

Хајде да сада мало детаљније размотримо услов при коме ће тело потонути:

Најпре ћемо заменити израз за силу потиска, а потом узети у обзир да се маса тела може израчунати помоћу формуле \(m=ρ V\) где је \(ρ\) густина тела, а math:V запремина тела.

Шта све можемо да скратимо у овом изразу?

Запремину и убрзање земљине теже.

И сада добијамо коначан услов при коме ће тело потонути:

Важи и обрнуто.

Пробај да одговориш на следећа питања ако су ти познате следеће густине:

Шта се дешава када тело не потоне?

У случају када је густина тела мања од густине течности (\(ρ < ρ_0\)), тело ће се наћи на површини течности и само један његов део биће уроњен у течност.

Последњих година са глобалним загревањем долази до отапања леда на половима, али и до одвајања огромних санти леда, које настављају да плове океанима и морима. Лед има мању густину од воде и због тога ледене санте плутају по површини. Ипак, највећи део леденог брега налази се испод површине. Хајде да израчунамо колика запремина је испод површине воде, ако знамо да цела ледена санта има запремину од \(1000m^3\), а да је густина леда \(ρ = 900kg/m^3\)

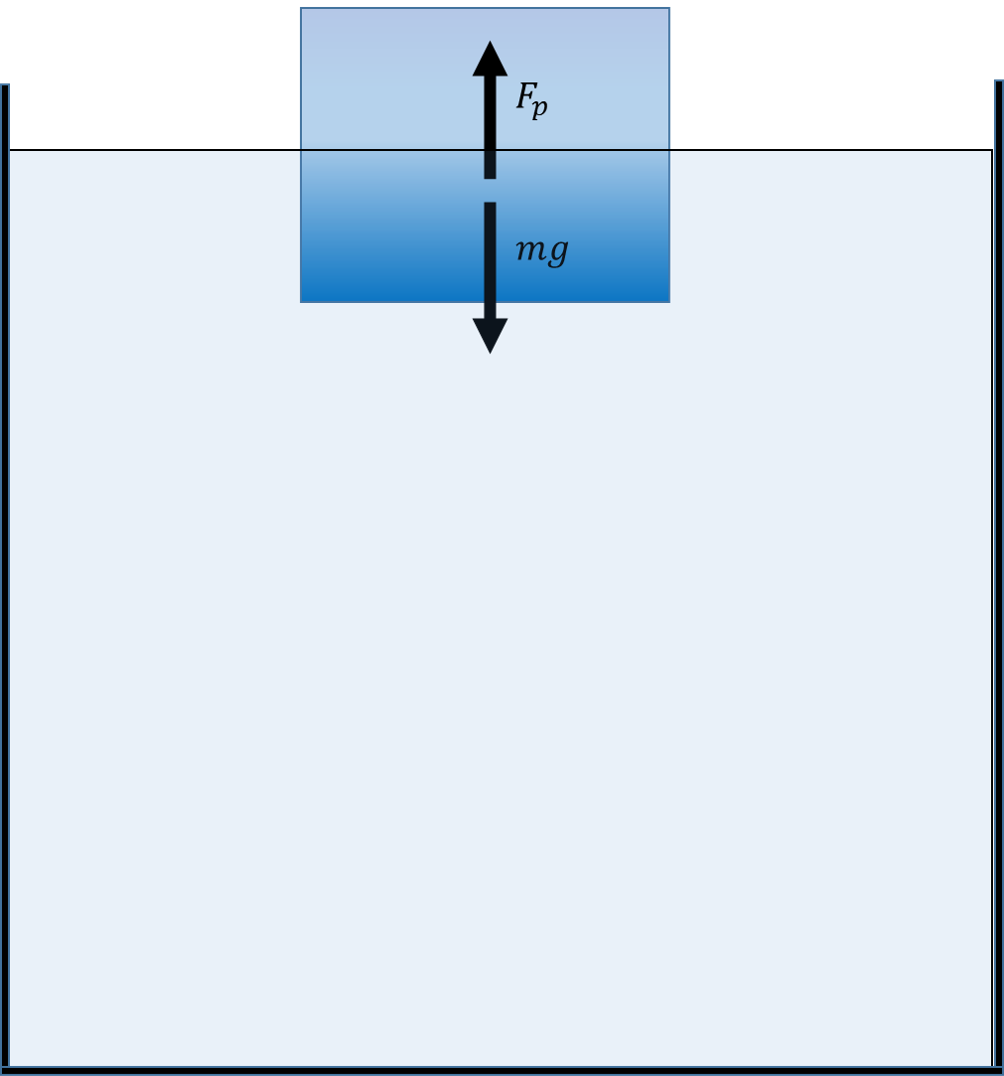
Најпре ћемо израчунати масу овог леденог блока:

А затим и силу теже која делује на њега:

Запитајмо се колика би сила потиска била потребна да делује на тело да оно не би потонуло?

Одговор је: иста као и сила теже. Сада, када знамо да је \(F_p = m g = 9~000~000N\), можемо да израчунамо запремину која се налази испод површине. Кренимо од:

где је \(V_1\) запремина леда испод површине воде. Добићемо:

Дакле, изнад воде се налази \(1m^3\), што је само десетина од укупне запремине.

6.1.4. Челични бродови¶

Како онда огромни бродови направљени од челика или других материјала могу да не потону, када је јасно да челик има већу густину од воде?

Ако поново погледамо симулацију, приметићемо следеће: како додајемо масу у наше буре, део који је под водом постаје све већи и већи.

Бродови су таквог облика да истискују огромну количину течности и тиме повећавају силу потиска. У случају брода, као густину треба узети масу брода подељену укупном запремином, која укључује и шупљине унутар брода. Овако израчуната густина је мања од густине воде.

На сличан начин деца која не умеју да пливају, остају више изнад површине уз помоћ надуваних гумених или пластичних „мишића” или појаса.

Хајде сада да се још подсетимо и тежине тела, коју смо учили прошле године.

На доњој слици представили смо разлику између силе теже \(mg\) и тежине тела \(Q\). Ако би се тело нашло у ваздуху без икакве подлоге испод њега, на њега би деловала сила \(mg\), али будући да нема подлоге, неће се јавити тежина \(Q\).

Са друге стране, тело које се налази на подлози (доле-десно) деловаће на подлогу тежином \(Q\)

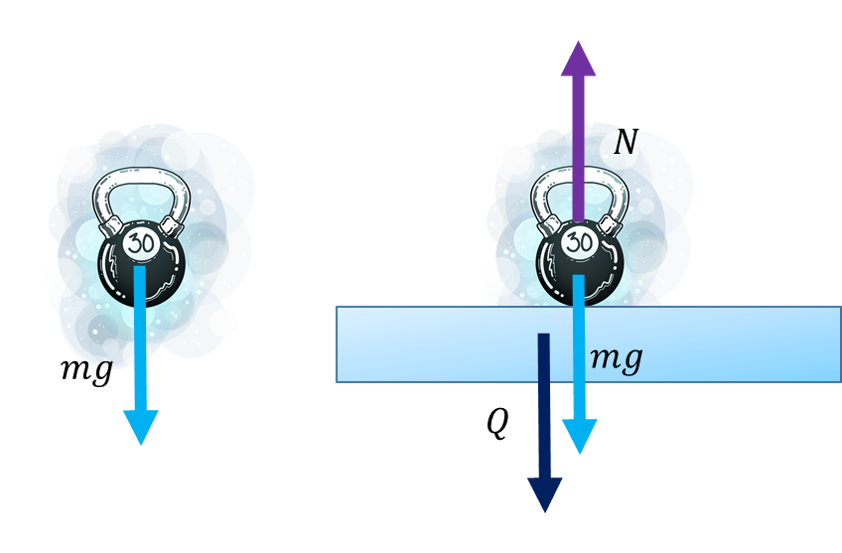
Ако би на тело деловала само сила теже, а оно стајало на подлози која мирује ове силе би биле једнаке по интензитету.

Али када се јави сила потиска, тежина тела ће се смањити управо за вредност силе потиска. Управо то ћемо демонстрирати у следећој симулацији.

У овој симулацији ћемо посматрати два идентична тела исте запремине и масе. Прво тело се налази у ваздуху, док је друго тело уроњено у течност. Тежину можемо мерити помоћу динамометра.

Пробај да извршиш симулацију за различите масе тела и густине течности.

Дакле, тело које се налази у некој течности изгубило је на својој тежини и ово се узима за тврдњу Архимедовог закона о сили потиска:

Наравно, ми смо током целе лекције помињали да је важно да тело буде уроњено у течност, али како онда објаснити оно што смо споменули на почетку лекције, односно балоне испуњене хелијумом и балоне испуњене обичним ваздухом?

Иако је ваздух око нас гас, а не течност, и он делује силом потиска на све ствари око нас. Зашто онда не примећујемо тај ефекат?

Одговор је у густини ваздуха. Она износи \(1,125 kg/m^3\), и ако упоредимо то са густином воде \(1000kg/m^3\) приметићемо да је тај број скоро 900 пута мањи, па је сам тим и сила потиска којом ваздух делује на нас 900 пута мања од оне коју бисмо осетили у води.

Наша маса је сувише велика да бисмо приметили ову силу. Али маса балона са хелијумом није тако велика (у односу на масу ваздуха исте запремине). Зато овде више не можемо да занемарујемо силу потиска којом ваздух делује на балон. Да ли сада имаш идеју зашто балон испуњен хелијумом лети? Да ли имаш идеју зашто користимо топао ваздух да бисмо управљали балонима?

Размисли и истражи шта се то дешава.

6.1.5. Закључак¶

Након ове лекције време је да сумирамо шта си научио/научила.

Најједноставније речено, свако тело уроњено у течност или гас губи на својој тежини за тежину истиснуте течности или гаса. Ово је познато и као Архимедов закон.

Сила која делује на тело уроњено у течност (или гас) назива се сила потиска.

И за крај, остали смо ти дужни остатак приче о Архимеду. Наиме, када је Архимед успео да открије закон по коме се понаша сила потиска, схватио је шта треба да уради како би решио проблем златне круне.

Тада је Архимед потопио златну круну у воду и измерио њену тежину. Потом је узео комад злата исте масе као круна и измерио његову тежину у води.

Уколико би круна била од чистог злата, имала би исту запремину као и комад злата те масе и на њих би деловала иста сила потиска. Ово би значило да би им и тежина у течности морала бити иста. Али, ако би се тежине разликовале, то би морало да значи да круна није од чистог злата.

Остављамо ти да истражиш ову причу и сазнаш да ли је круна била златна или је имала и сребра у себи.