3.1.1. Више сила није већи проблем¶

Да ли на тело мора да делује само једна сила?

Одговор је не.

Други Њутнов закон је лако применити када на тело делује само једна сила. На пример:

Али шта ћемо са много реалнијим случајем када на тело делује више сила истовремено?

Како решити задатак у коме на једно тело делују две или више сила?

Управо то ћеш научити у лекцији која следи.

Овога пута инспирацију за одговор ћемо потражити у морима и океанима.

Још у давна времена људи су били морепловци. Временом су цивилизације у југоисточној Азији правиле све снажније и брже бродове који су могли да плове све даље и даље захваљујући једрима. Ово је било неопходно, јер су живели од улова рибе и краба и добар брод је представљао разлику између доброг и лошег улова. Стари Египћани су први научили како да споје даске у тело брода и били су познати по овој техници, која је бродоградњу учинила лакшом.

Грци су имали снажну морнарицу коју су користили за трговину, али и у ратовима. Нарочито је Атина била поносна на своје бродове и луке. Не можемо никако да занемаримо Викинге који су се толико извештили у бродоградњи да су успевали да пређу океан, о чему сведоче и насеља викинга у северној Америци.

Зашто спомињемо бродове са једрима?

Зато што су они одличан пример како две силе могу деловати на тело.

О томе зашто бродови плутају на површини учићете у лекцији о сили потиска. Тада ћемо разматрати силе које делују дуж вертикале. Међутим, нас у овој лекцији више интересују силе које делују на брод у хоризонталном правцу, јер оне могу да доведу до промене брзине брода.

Сада ћемо посматрати једну викиншку лађу која поред једара користи и весла. О томе колико су Викинзи били срећни када су морали да веслају причаћемо неком другом приликом.

3.1.2. Слагање силa које делују у истом правцу¶

Посматрајмо следећу ситуацију. Викиншки брод је наишао на мирно море. Отворили су једра и ветар је почео да делује неком силом $F_v$ на њих. Ипак Викинзима се жури и они желе да добију већу брзину, дакле желе веће убрзање, тако да морају да почну да веслају и да на брод делују силом $F$.

Хајде да видимо у следећој симулацији шта се дешава када Викинзи и ветар раде заједно.

Пробај да одговориш на следећа питања:

Шта се дешава са убрзањем када Викинзи почну да веслају?

Да ли ове две силе „помажу“ једна другој?

Пробај да помоћу другог Њутновог закона израчунаш силу која делује на брод (маса пута убрзање) и упоредиш је са збиром сила ветра и Викинга. Шта примећујеш?

Из овог последњег питања можеш да закључиш да тело добија убрзање као да на њега делује једна сила која је једнака збиру свих сила које делују на њега.

Ова сила се назива и резултујућа сила или скраћено резултанта $F_r$.

Постоје бројни примери оваквог деловања сила. Рецимо два човека који заједнички гурају аутомобил:

Теретни пси који вуку санке:

Вероватно најпознатији пример је садржан у бајци о Деди и репи.

Када добијемо резултујућу силу лако је применити други Њутнов закон, баш као у питању са почетка лекције. Хајде да ово проверимо на једном задатку.

Марко и Весна покушавају да на глаткој подлози помере кауч заједно и делују на њега силама у истом правцу и смеру. Ако Марко делује силом од $15N$, а Весна силом $20N$ коликo ће убрзање имати кауч ако му је маса 70 $kg$?

Задатак ћемо решити тако што ћемо најпре одредити резултујућу силу:

$F_r= F_1 + F_2 = 15N+ 20N= 35N$

Потом ћемо применити други Њутнов закон и израчунати убрзање:

$a = F_r/m= 35N/70kg = 0.5m/s^2$

Пробај да следећи задатак урадиш сам.

Али шта ако две силе делују у истом правцу, али у супротним смеровима?

Погледајмо сада симулацију у којој су наши храбри Викинзи налетели на морску струју која делује силом $F_s$ у смеру супротном од оног у коме они желе да иду. Сада немају избора него да се дохвате весала и почну да веслају силом $F$.

Пробај да помогнеш Викинзима и успут даш одговоре на следећа питања:

Шта се дешава са убрзањем када Викинзи почну де веслају?

Пробај да помоћу Њутновог закона израчунаш силу која делује на брод (маса и убрзање су дати у симулацији) и упоредиш је са силама која делују на брод. Шта добијаш?

Овога пута резултујућа сила једнака је разлици сила која делују на тело, док је њен смер исти као и смер веће силе.

Пример овог деловања представљен је на следећој слици:

У шестом разреду си учио/учила о сили трења (у овом курсу ћемо ускоро учити детаљније о овој сили), и тада је речено да је реч о сили која се супроставља кретању тела у односу на подлогу. Управо такав пример је дат на претходној слици. Весна покушава да помери кауч масе $m=75kg$ и делује на њега силом $F_2=20N$, али је омета сила трења $F_t = 5N$.

Резултујућу силу сада тражимо као разлику ових сила. Будући да је $F_2>F_t$ резултујућа сила имаће смер силе $F_2$

Даље се добија:

У наредних неколико примера покушај да самостално даш одговор.

3.1.3. Слагање две силе које делују у међусобно нормалним правцима¶

Овога пута оставићемо Викинге, а ми ћемо се запутити у свемир.

Посматраћемо један мали свемирски брод. У свемиру нема ни воде ни ветра, па не можемо да користимо једра или весла, али зато наш брод има четири ракетна погона, по један са сваке стране брода. Ови ракетни погони обележени су словима A, B, C и D. Сваким од ових погона може се управљати тако што подешавамо интезитет силе којом он делује на брод.

Хајде да посматрамо шта ће се десити.

Шта се дешава када укључимо само погон А?

Шта се дешава када укључимо само погоне А и C? (подесите да силе буду различите)

Шта се дешава када укључимо погоне А и B истовремено?

Истражи шта се дешава за различите комбинације укључених потисака.

Овога пута резултујућу силу наћи ћемо помоћу Питагорине теореме.

Најпре да објаснимо шта се догодило и како се добија резултујућа сила у овом случају. Наиме, ако нацртамо силе које делују на тело у међусобно нормалним правцима:

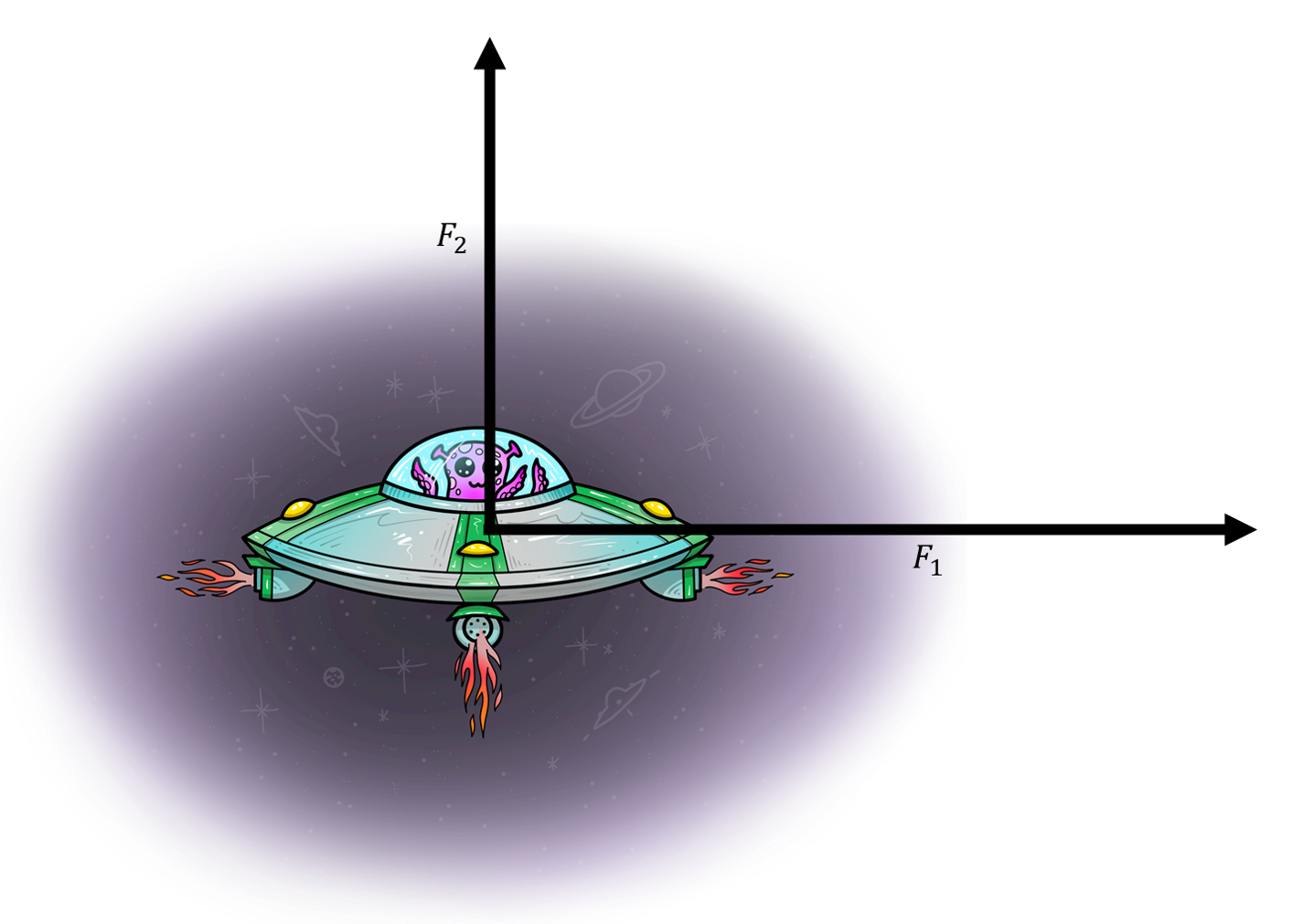
Потом из њихових крајева повучемо још две линије које су паралелне са правцима у којима силе делују. Oве линије су на слици испрекидане.

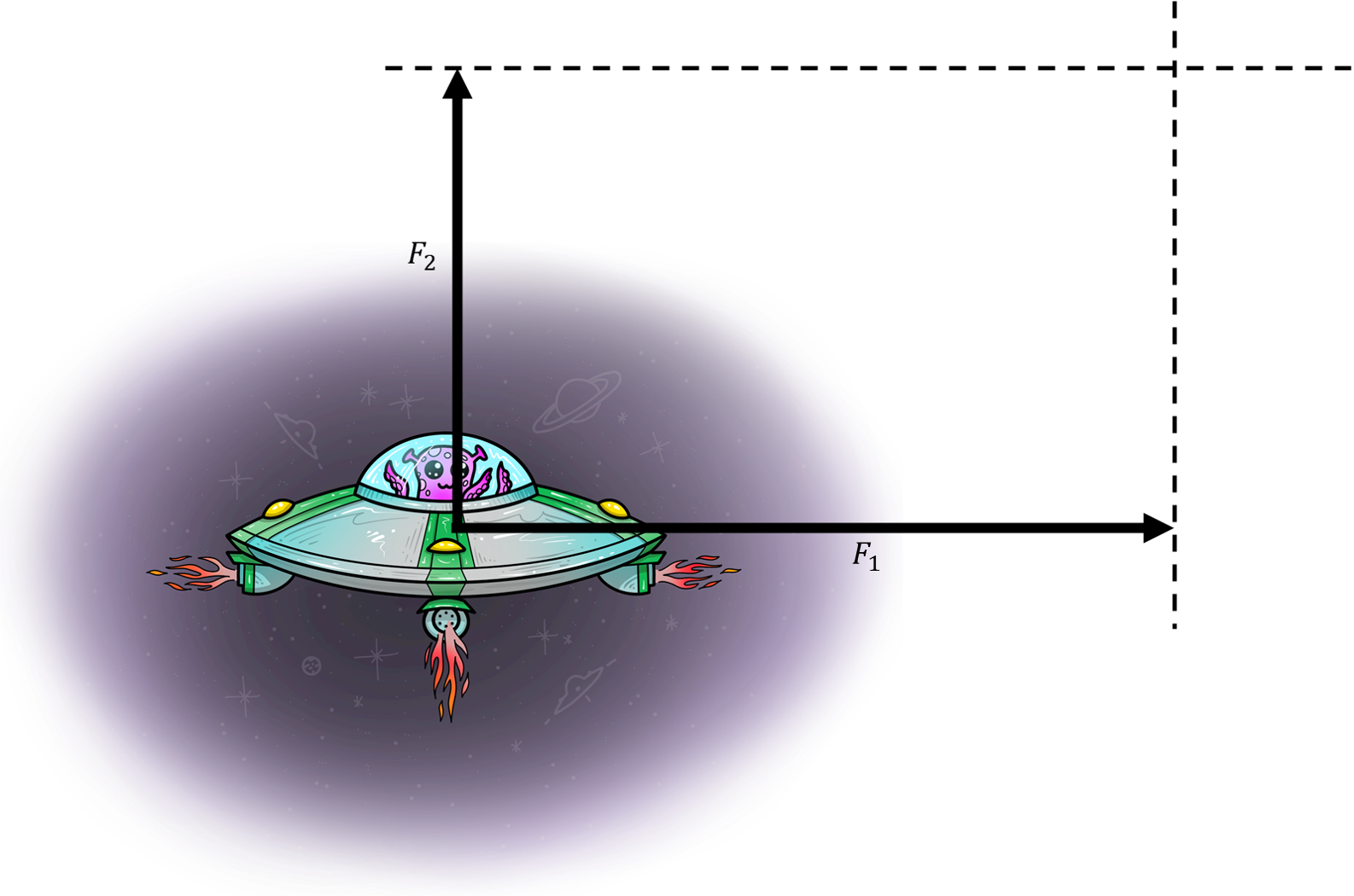
Испрекидане линије заједно са векторима сила чине правоугаоник. Уочи дијагоналу правоугаоника.

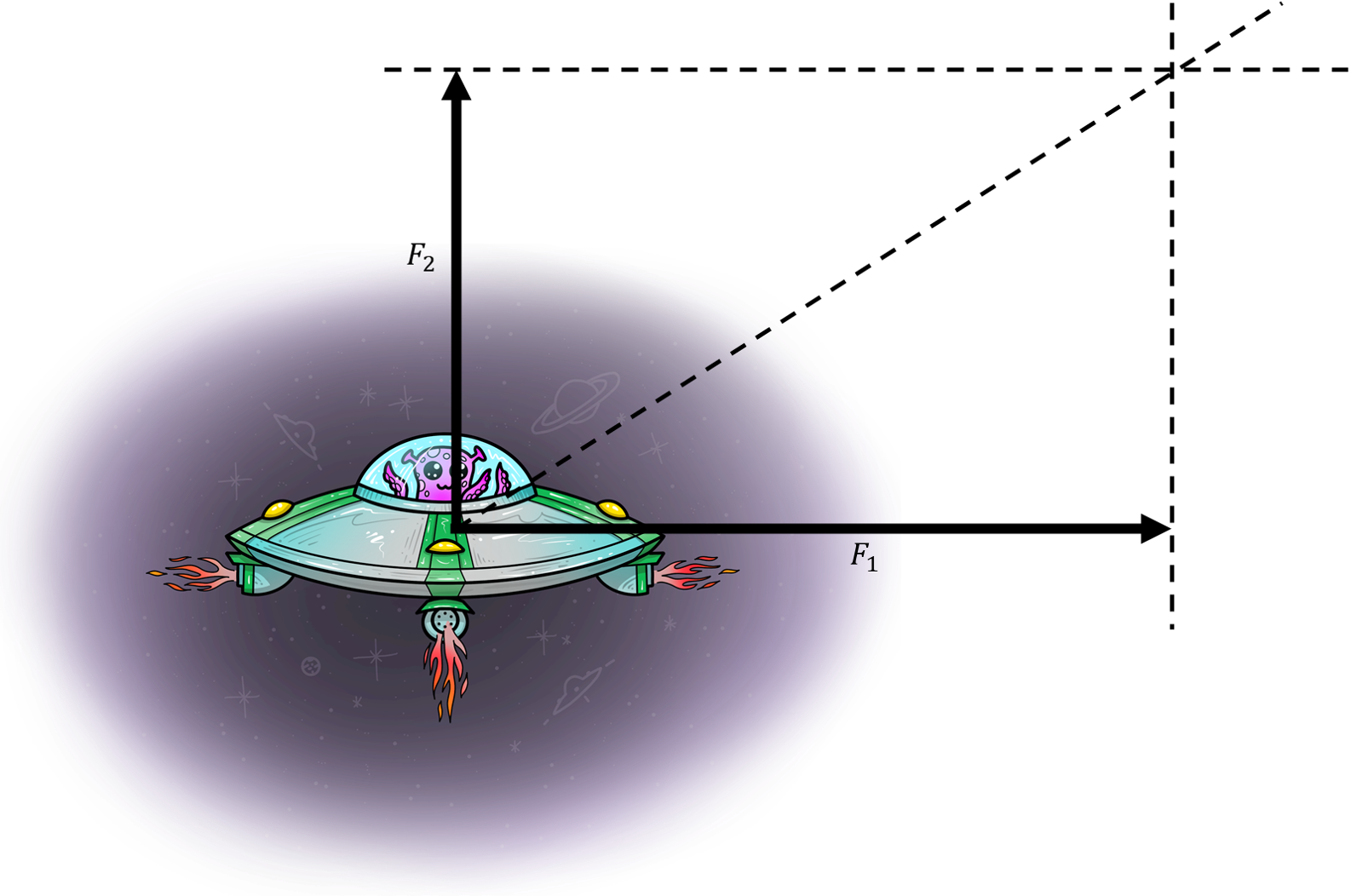
Резултујућа сила има правац дуж дијагонале. Њен вектор почиње у заједничком почетку сила $F_1$ и $F_2$ а завршава се у тачки у којој су се пресекле линије које смо повукли.

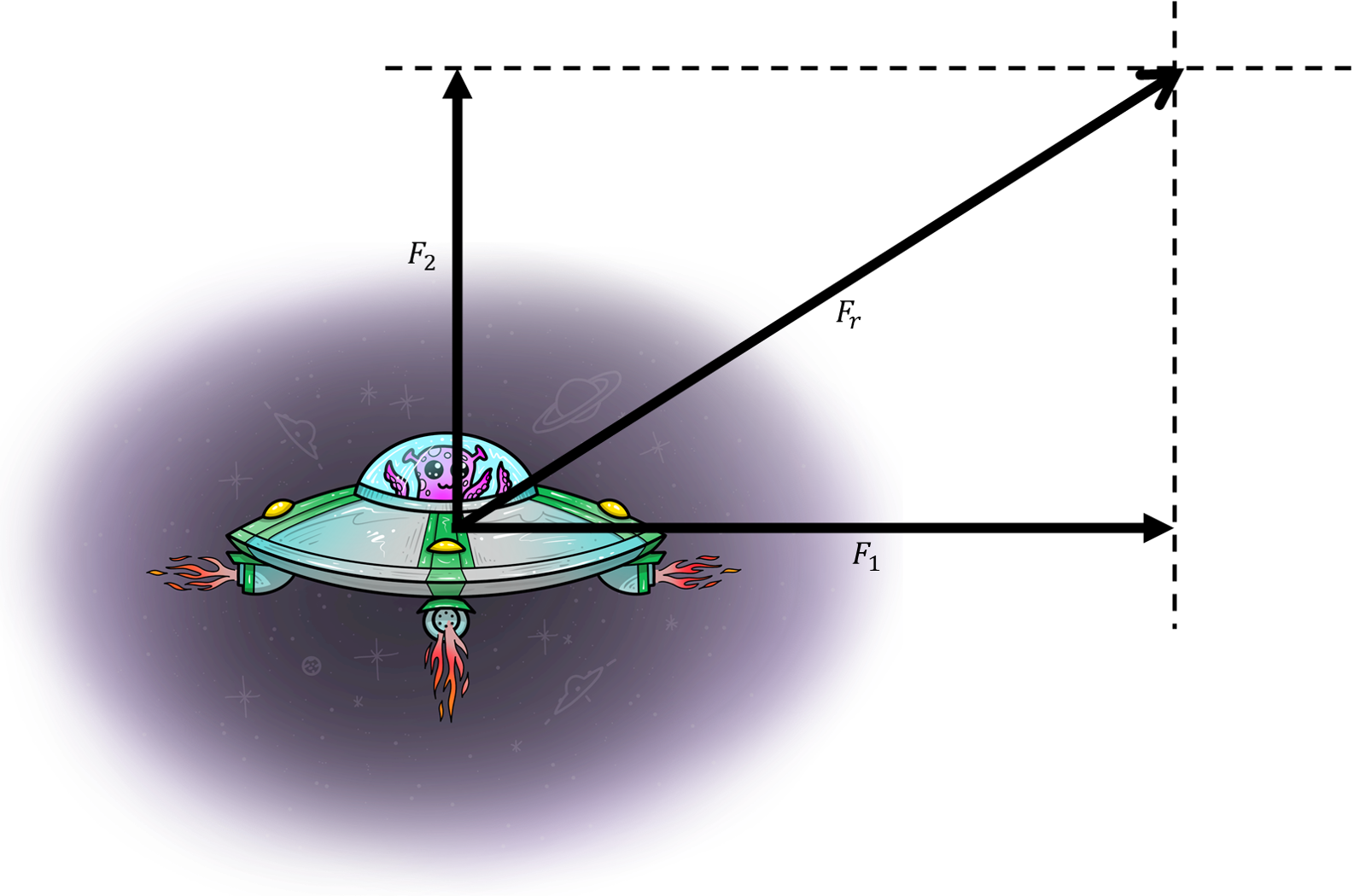
Сада можемо да применимо Питагорину теорему на правоугли троугао (знамо да су код правоугаоника супротне странице једнаке) како бисмо израчунали и интензитет силе.

Како то изгледа на примеру?

Претпoставимо да наш свемирски брод масе $1000 kg$ делују две силе у међусобно нормалним правцима $F_1 = 2000 N$ и $F_2 = 2000 N$

Најпре ћемо да применимо Питагорину теорему на векторе сила:

Oдакле кореновањем и заокруживањем добијамо приближну вредност резултанте:

Сада можемо да применимо други Њутнов закон

Покажи нам колико си разумео/разумела ову лекцију тако што ћеш подесити силе свемирског брода (користећи знање о Питагориним паровима које си учио/учила на часу математике) и решити следеће проблеме:

Капетан свемирског брода укључује погон A и намешта интезитет силе на $40kN$. Истовремено укључује и погон B на коме намешта интезитет силе од $30kN$. Колики је интезитет резултујуће силе?

А шта ако подеси погон C на $12kN$, а погон D на $5kN$? Колика је сад резултујућа сила?

3.1.4. Тест¶

Да ли си спреман/спремна за један мали тест?

Не брини, није за оцену, већ само да проверимо колико си разумео/разумела градиво.

У ком смеру делује ова сила?

И последњи (и најтежи) задатак за ову лекцију.

3.1.5. Закључак¶

У овој лекцији научили смо да више сила не значи и већи проблем. Кад на једно тело делује неколико сила можемо да их заменити једном која се назива резултујућа сила.

У случају да силе делују дуж истог правца и смера сабраћемо их:

У случају да силе делују дуж истог правца, али супротног смера одузећемо их:

У случају да силе делују дуж међусобно нормалних праваца, најпре ћемо конструисати паралелограм , а потом помоћу Питагорине теореме израчунати резултујућу силу: