2.1.1. Ромео, Јулија и сва та физика¶

Данашњу причу о физици почињемо у Верони. Верона је прелеп град у Италији, али за разлику од Пизе и Фиренце (градова у којима је живео Галилео) није толико чувен по науци, колико је по Ромеу и Јулији. Они су јунаци једне од најпознатијих љубавних трагедија чувеног енглеског писца, Вилијама Шекспира.

Ми нећемо даље причати о Шекспиру, ипак је ово курс физике, али ћемо искористити једну од његових сцена, која спада у најпознатије сцене у драматургији, како бисмо научили нешто више о кретању у гравитационом пољу Земље.

У овој сцени Ромео се налази испод Јулијиног балкона. Ромео је дошао кришом (јер морају да крију своју љубав од Јулијиног тате) и покушава да Јулији добаци ружу коју је убрао. Хајде да размотримо ово у симулацији и видимо шта се дешава.

У овој симулацији можеш да мењаш брзину којом Ромео избацује ружу вертикално навише ка Јулији.

Пробај да помоћу симулације одговориш на следећа питања:

2.1.2. Хитац навише¶

Кретање под утицајем силе Земљине теже (силу отпора ваздуха ћемо, као и у претходној лекцији, занемарити) у коме телу саопштимо почетну брзину вертикално навише зове се хитац навише.

О томе шта се дешава када укључимо и силу отпора ваздуха учићемо у некој од наредних лекција.

Ако погледамо слику, можемо видети да на тело делује сила теже супротно од почетне брзине. Према томе ово је успорено кретање. У претходној симулацији могли смо да закључимо на основу тога што је бачени предмет ишао све спорије и спорије док се коначно није зауставио. Након тога под дејством силе теже овај предмет почиње да пада (о томе смо учили у претходној лекцији).

Будући да је једина сила која делује на тело \(mg\), применом другог Њутновог закона добијамо (слично као за слободан пад) да је убрзање тела \(g= 10 m/s^2\)

Сада је врло лако применити једначину за брзину (закон брзине) за равномерно промењиво кретање.

Ако заменимо убрзање \(a\) са \(g\) и узмемо у обзир да тело успорава, па користимо знак \(-\) уместо \(±\), добићемо формулу по којој можемо рачунати тренутну брзину тела за хитац навише.

Хајде да применимо научено на примеру.

Ако Ромео баци ружу вертикално навише брзином од \(5m/s\) колика је брзина руже након \(0.4 s\) ?

\(v_0 = 5 m/s\)

\(t = 0.4 s\)

Сада када смо извукли податке можемо приступити рачунању.

Следеће задатке покушај да урадиш самостално.

Приликом сервиса у одбојци примач покушава да подигне лопту увис како би свом тиму дао више времена да организује акцију. Лопта је сервирана, Ана је дочека исправно и након тога лопта се одбије од њених руку вертикално навише почетном брзином 15m/s. Будући да је кретање лоптe након одбијања од Анинe руке хитац навише, а да ћемо због лакшег рачунања за убрзање Земљине теже узети вредност \(g=10 m/s^2\) покушај да одговориш на следећа питања:

МАЛИ КВИЗ О ОДБОЈЦИ:

Обрати пажњу на један детаљ: брзина коју смо израчунали у тренутку t=2 s је негативна. Ово није ништа необично. Реч је о томе да је лопта почела да пада. Негативна вредност брзине у овом случају значи да је тело променило смер кретања у односу на почетни смер.

Нама је посебно занимљиво треће питање. Ако се вратимо на симулацију, приметићемо да у моменту када се лопта заустави, она је истовремено и на највишој висини. Ово је и логично, јер да у том моменту брзина није једнака нули, тело би или наставило да се креће и достигло већу висину, или наставило са падањем што би значило да је пре тога било на већој висини.

Али како да одредимо тренутну висину тела код хица навише?

Ако погледамо слику, приметићемо да је пређени пут тела једнак висини на којој се тело налази (умањеној за почетну висину ако хитац није са земље).

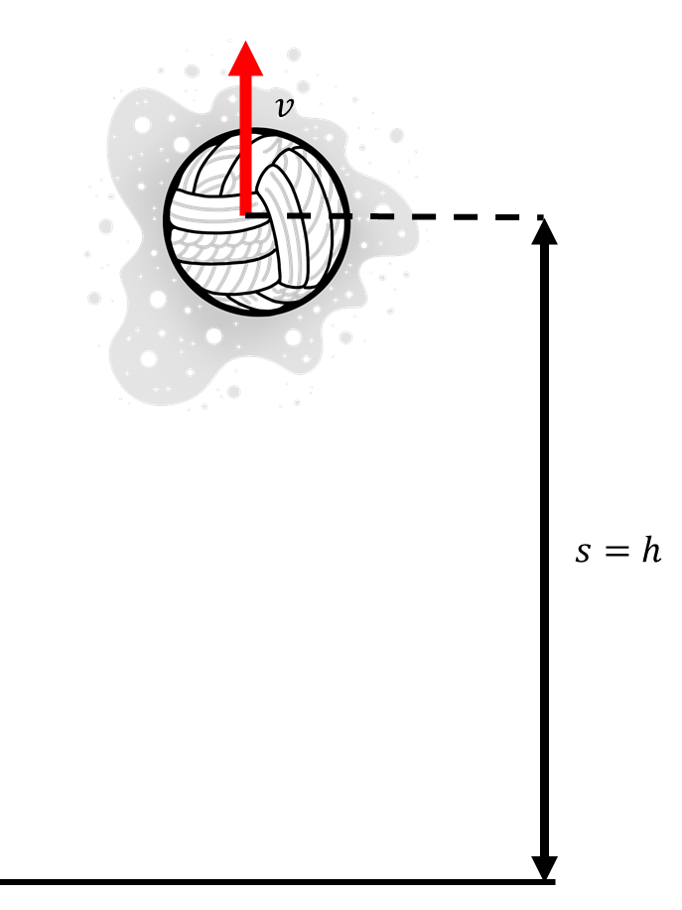
Ако применимо формулу за пређени пут код равномерно промењивог успореног кретања

и уврстимо да је убрзање тела заправо \(g\), (као и да су пређени пут и висина на којој се тело налази једнаки \(s=h\) ), добићемо формулу за тренутну висину код хица навише.

A како да одредимо максималну висину \(H\) коју ће тело достићи?

Сада ћемо применити формулу за зависност тренутне брзине од пређеног пута код равномерно промењивог кретања.

Будући да знамо да убрзање \(a\) замењујемо са \(g\) , као и да је кретање успорено добијамо:

Већ смо закључили да у тренутку када је висина максимална \(h=H\), тренутна брзина је једнака нули \(v=0m/s\), тако да сада долазимо до формуле за максималну висину тела

или ако мало средимо израз:

Приметићемо да максимална висина зависи од почетне брзине тела.

Сада можемо израчунати висину до које је стигла ружа коју је Ромео у претходном задатку бацио. Најпре ћемо извући улазни податак:

\(v_0 = 5 m/s\)

Сада можемо приступити рачунању:

До истог резултата можемо да дођемо ако прво помоћу формуле \(v = v_0 - g \cdot t\) израчунамо време потребно да се ружа заустави. У тренутку заустављања руже њена брзина је 0 (\(v = 0\)), па имамо:

Сада применом формуле \(h = v_0t - {gt^2\over 2}\) добијамо:

МАЛИ КВИЗ О ОДБОЈЦИ 2

У претходном примеру Ана је успела да лопту усмери вертикално навише почетном брзином од \(15m/s\). Висину ћемо мерити у односу на Анине руке. Одговори на следећа питања:

Приметићете да у одговору на друго питање тело је већ почело да пада, али ми не морамо да мењамо формулу. Како време пролази висина ће најпре постајати све веће већа и већа, достићи неку максималну вредност и након тога почети да се смањујe. Тада кажемо да је тело почело да пада.

2.1.3. Закључак¶

У овој лекцији смо посматрали другачије кретање у гравитационом пољу у односу на слободан пад који смо проучили у претходној лекицји.

Кретање под дејством силе теже са почетном брзином усмереном вертикално навише назива се хитац навише.

У питању је праволинијско равномерно успорено кретање, какво си већ учио/учила на почетку седмог разреда.

Ово кретање смо упознали кроз кретање руже коју Ромео добацује Јулији, као и посматрањем кретања одбојкашке лопте која се после пријема сервиса одбила вертикално навише. Али постоје и други примери попут:

• судијског подбацивања лопте на почетку кошаркашке утакмице.

• припреме тенисера да изведе сервис када баци лоптицу у ваздух.

• гејзир или фонтана који избацује воду вертикално увис.

Примени оно што смо научили.

Ромео жели да добаци ружу Јулији. Ако баци ружу превише брзо, она ће проћи поред Јулије толико брзо да она неће успети да је ухвати, али ако баци ружу сувише споро ружа неће ни стићи до Јулије. Пробај да израчунаш брзину којом Ромео треба да баци ружу до Јулије да би она постигла максималну висину у моменту када стигне до ње.

Примети да у овој симулацији можеш да мењаш висину до које треба да стигне ружа. Тачније, можеш да задаш разлику висина између Ромеове и Јулијине руке, то јест пут који треба да пређе ружа. Симулацију можеш да користиш овако: прво изабери висину, затим израчунај потребну почетну брзину и на крају унеси израчунату брзину и покрени симулацију да провериш резултат.

2.1.4 Тест¶

Ако си пажљиво пратио/пратила лекцију и радио/радила задатке онда нећеш имати проблема ни са задацима који следе. Понављамо још једном ово је супер припрема за завршни испит, па и ако погрешиш, не брини, јер је и то део учења.

А сад два тешка питања (за праву петицу)