Садржај
Увод у симулације
Кинематика транслаторног кретања
Динамика транслаторног кретања
Кинематика ротационог кретања
Динамика ротационог кретања кретања
Закључак
Евалуација
Сила трења¶
Природа силе трења је доста сложена. Када говоримо о сили трења у оквирима школског градива, ми се задржавамо на њеним макроскопским особинама (ономе што видимо да сила трења ради), а не улазимо у њено микроскопско описивање (објашњења настанка силе трења залазећи у молекулски ниво). Такође, у овој лекцији ћемо се концентрисати на тзв. суво трење, тј. трење које се јавља између чврстих површина. Трење постоји и између чврстих и течних површина, као и између слојева течности. У том случају говоримо о вискозном трењу.
Када говоримо о сувом трењу, разликујемо трење клизања и трење котрљања. У овој лекцији ћемо се задржати на трењу клизања. Трење се јавља и у случају када тело мирује а на њега делује сила која покушава (али још увек не успева) да га изведе из стања мировања. Тада говоримо о сили трења мировања тј. статичкој сили трења.
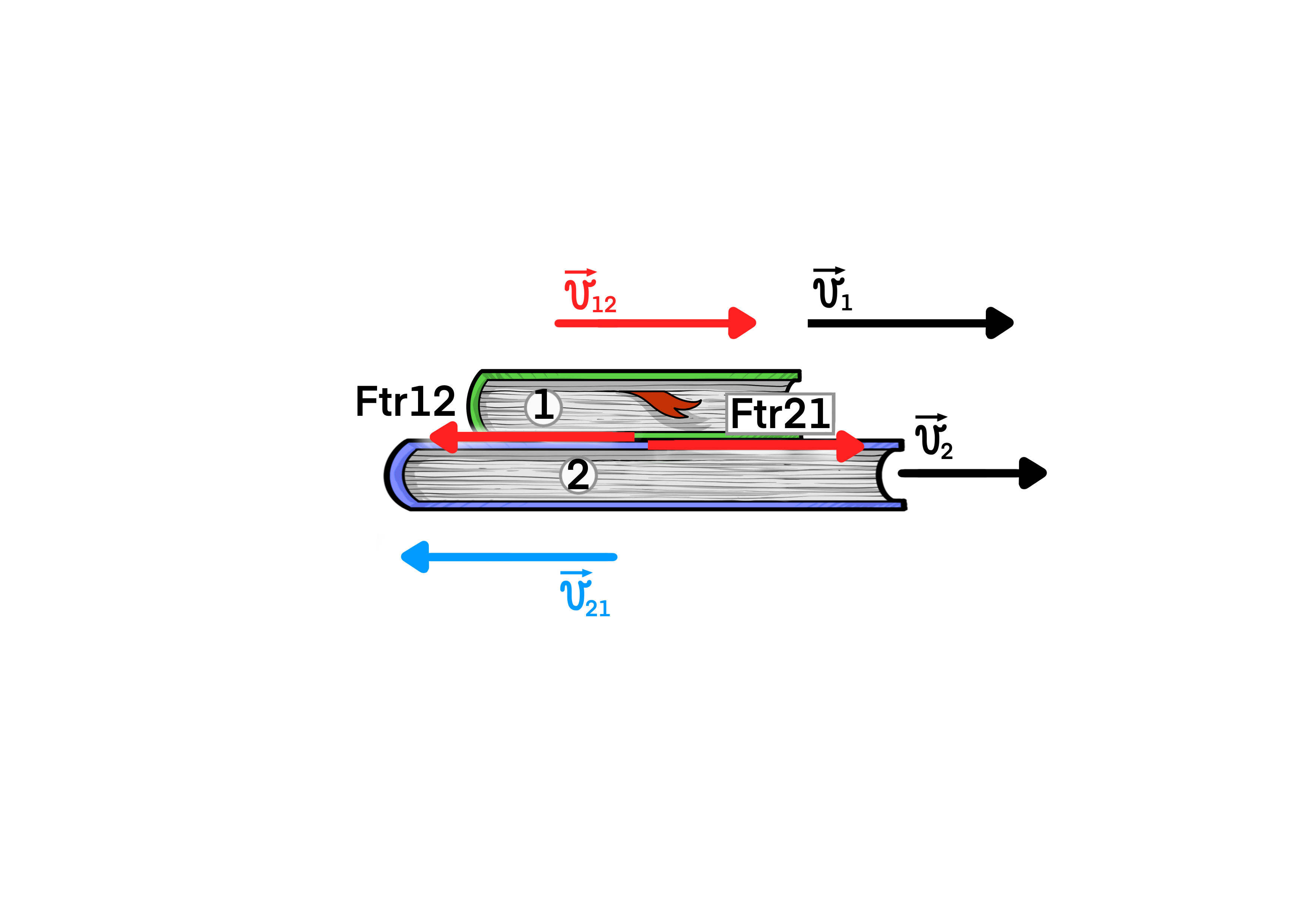
Посматрајмо једноставан пример у коме на столу имамо књигу преко које је још једна књига. Прстом гурамо горњу књигу и гледамо шта се дешава када мењамо интензитет силе гурања.
Из искуства знамо да ако књигу не гурнемо довољно јако, нећемо је покренути. Ако је гурнемо довољно јако може да се деси да покренемо само горњу књигу, а може да се деси и да покренемо обе књиге.
У следећој симулацији можеш да мењаш интезитет сила и да видиш шта се дешава са књигама:
Можемо да приметимо да докле год сила не достигне неку минималну вредност \(F_{min}\), књига неће да се покрене. Тело се не креће иако на њега делујемо силом. Други Њутнов закон нам каже да је то једино могуће ако на то исто тело делује сила истог интезитета а супротног смера. Књига 1 је једино још у контакту са књигом 2, што значи да једина сила поред оне којом вучемо тело може да потиче од књиге 2. Та сила којом књига 2 делује на књигу 1 и која се супроставља кретању је сила трења мировања. Минимална вредност силе којом можемо да вучемо књигу 1 а да се она не помери је уствари максимална вредност силе трења мировања (\(F_{min}=F_{stmax}\)). Максимална сила трења мировања зависи од тога какве су површине које се додирују (колико су храпаве односно глатке) и од силе којом једно тело нормално притиска друго. То записујемо на следећи начин: \(F_{stmax}=\mu \cdot N\), где је \(N\) сила нормалног притиска једног тела на друго (по интезитету, због Трећег Њутновог закона сила којом књига 1 притиска књигу 2 је једнака сили којом књига 2 притиска књигу 1), а \(μ_s\) је коефицијент статичког трења. Овај коефицијент садржи информацију о томе какве су површине које се додирују, нарочито о томе колико су храпаве.
Ако смо успели да покренемо горњу књигу, обе књиге ће се кретати заједно све док сила којом не достигне неку нову граничну вредност, коју можемо да нађемо из следећег:
Једначина кретања за горњу књигу:
Једначина кретања за доњу књигу:
Овде је сила трења и даље сила трења мировања, па важи
Комбиновањем две једначине и неједначине, добијамо да докле год интезитет силе којом гурамо горњу књигу задовољава услов
обе књиге се крећу заједно.
Када сила којом гурамо горњу књигу постане већа од \(\mu \cdot \frac {m\cdot(m+M)} {M} \cdot g\), свака књига ће се кретати за себе, односно постојаће релативно кретање једне књиге у односу на другу.
Ни овде не смемо да заборавимо Трећи Њутнов закон (закон акције и реакције) захваљујући коме знамо да ако тело 2 делује на тело 1 неком силом, онда и тело 1 мора да делује на тело 2 силом истог интезитета и правца али супротног смера. То значи да се јавља реакција силе трења \(F_{tr12}\) сила \(F_{tr21}\). Ова сила сада покушава да покрене доње тело.
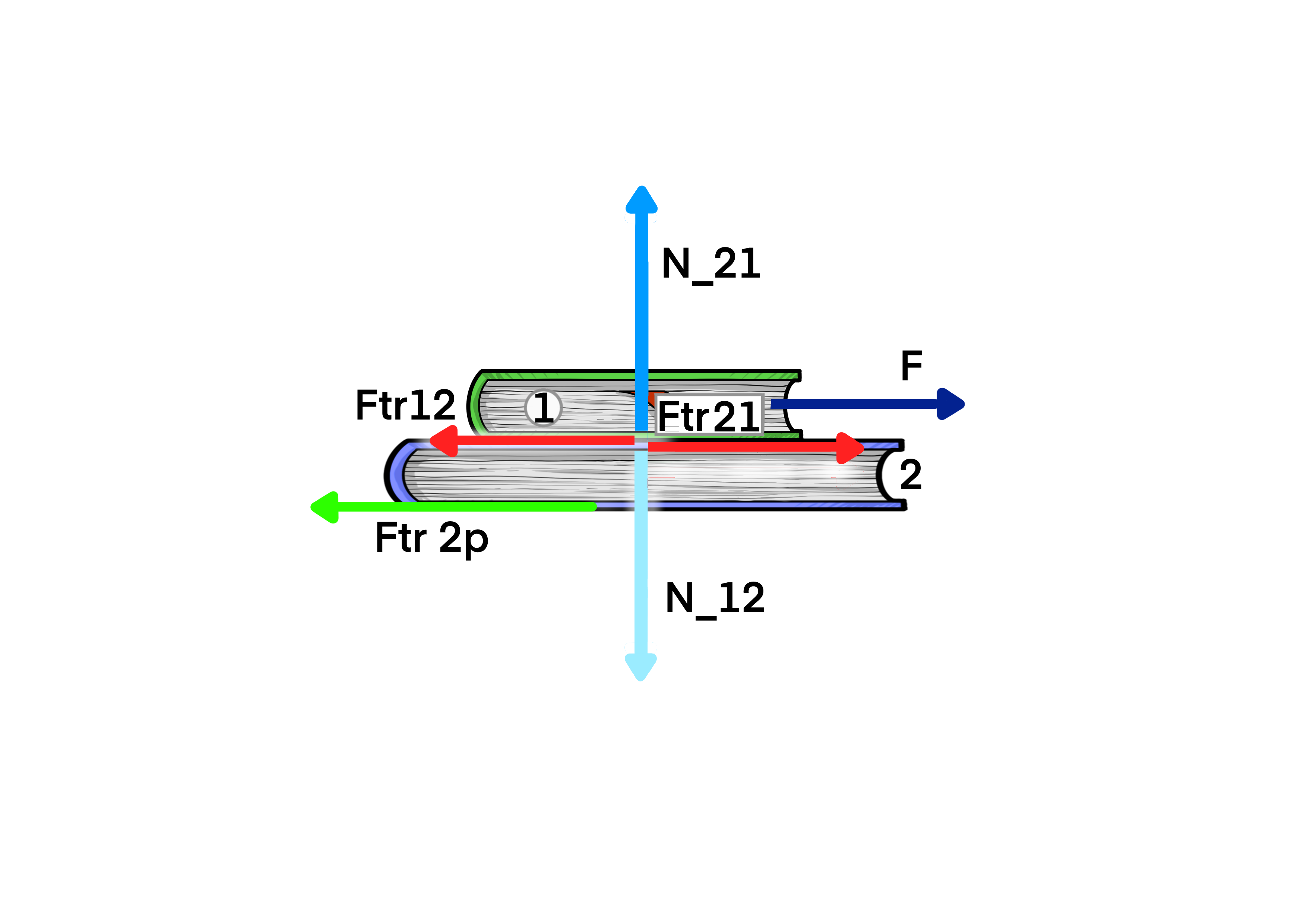
Док год је сила трења \(F_{tr12}\leq \mu \cdot N\) тела се крећу заједно (нема релативног кретања једног у односу на друго).
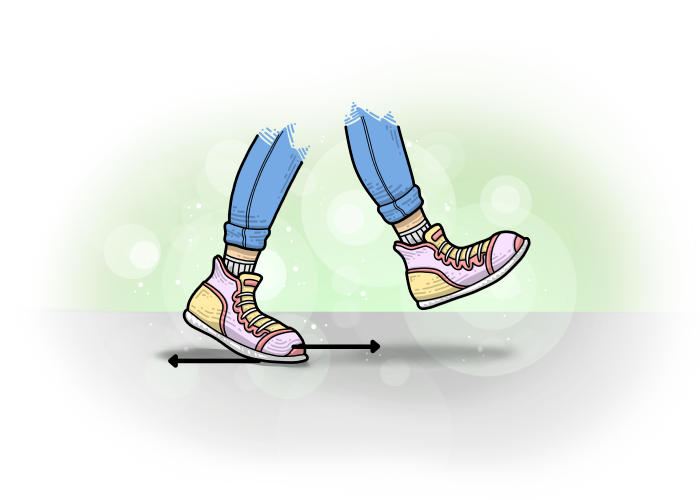
Примери силе трења мировања: Када ходамо или трчимо, ногом којом се ослањамо о подлогу ми потискујемо подлогу уназад, па подлога на ту ногу (због Трећег Њутновог закона) делује силом која је по својој природи сила трења мировања (јер се нога која је ослонац не креће).
Када наслонимо предмет на зид, тај предмет стоји захваљујући сили трења мировања. Захваљујући сили трења можемо да ставимо тело и на површину која је коса, статичка сила трења ће га задржавати да не падне под дејством компоненте силе Земљине теже.
Погледај шта се дешава са књигом на полици у следећој симулацији.Можеш да укључиш и искључиш силу трења и да видиш какви су ефекти.
Kaда сила којом вучемо постане већа од максималне силе трења мировања, тело се креће. Сила трења и даље постоји, али сада је то динамичка сила трења (сила трења кретања). И динамичка сила трења (слично статичкој) зависи од силе нормалног притиска једног тела на друго и од храпавости површина. Ова друга информација садржана је у тзв. динамичком коефицијенту трења, па можемо да запишемо да је \(F_{tr}=\mu \cdot N\). Сила трења клизања не зависи од величине додирне површине између тела.
Koeфицијент динамичког трења је код већине материјала нешто мањи од коефицијента статичког трења. Такође, коефицијент динамичког трења није у потпуности константан, тј зависи од релативне брзине тела. Зависност коефицијента динамичког трења од брзине можемо сматрати малом. Такође, за већину случајева које ћемо ми разматрати можемо да сматрамо и да је разлика динамичког и статичког коефицијента трења мала. Дакле, најчешће са довољно добром тачношћу можемо да узмемо да је коефицијент динамичког трења константан и да је једнак коефицијнету статичког трења. Дакле, у већини случајева ћемо говорити о једном коефицијенту трења, тј. \(\mu_d=\mu_s=\mu\).
Утицај подлоге по којој се тело креће тј утицај коефицијента трења можемо да видимо у следећој симулацији.
Дечак вози електрични тротинет. Испред себе види раскрсницу и хоће да се заустави, па искључи мотор и примени кочнице. Сматрамо да кочнице заблокирају точкове, тако да је ротације точкова онемогућена и тротинет се креће само транслаторно.
Колико времена пре раскрснице треба да закочи ако се креће по асфалту, мокром асфалту, снегу, леду? Мењањем коефицијента трења у симулацији можеш да утврдиш кад је зауставно време највеће, а када је најмање.
Од тренутка када је почео да кочи, на тротинет делује само динамичка сила трења клизања која га успорава до заустављања. Да ли је почео да се зауставља на време ако је раскрсница од његовог положаја кад је почео дао кочи удаљена за растојање \(d\)?
Закључујемо да је зауставно време обрнуто пропорционално коефицијенту трења \(\mu\). Што је коефицијент трења већи, зауставно време ће бити мање односно што је површина храпавија, тротинету ће бити потребно краће време да се заустави.
Да би се зауставио на време треба да важи \(s_z\leq d\).
Видели смо да динамичка сила трења зависи и од силе нормалног притиска једног тела на друго. Сила нормалног притиска је већа уколико је већа маса тела. Ипак, успорење при кочењу не зависи од масе, што ћемо видети у следећој симулацији.
У следећој симулацији имамо истог дечака који вози електрични тротинет као у претходној симулацији. Можеш да додајеш масу ранца на масу дечака.
Колико времена пре раскрснице треба да закочи ако се дечак вози без и са ранцем са књигама? Маса дечака са тротинетом је \(m\), а маса ранца са књигама је \(m_1\).
Слично претходном примеру, када тротинет кочи (при чему подразумевамо да точкови не ротирају када су закочени), једначина кретања тротинета са дечакаом без ранца је
Када се дечак вози са ранцем једначина кретања тротинета постаје
Показали смо да успорење при кочењу тротинета не зависи од масе која је на њему.
Покушај сада да решиш следећи задатак:
Дечак стоји на скејтборду који се креће по подлози. Колико може да буде максимално убрзање скејтборда да дечак и даље може да стоји на њему?

Сила која покреће скејтборд (сила вуче) доводи до убрзаног кретања скејтбода и он се креће убрзањем \(а\) које је усмерено на десно. И дечак се креће на десно, заједно са скејтбордом, односно истим убрзањем. Једина сила која делује на дечака је сила трења и она делује на десно. Наиме, то је сила реакције која се јавља између дечака и скејтборда: сила трења којом дечак делује на скејтборд је усмерена на лево, а сила којом скејтборд делује на дечака усмерена је на десно.
Дечак неће пасти са скејта све док се креће заједно са њим тј све док су убрзања скејтборда и дечака једнака. То ће бити испуњено све док је сила трења између дечака и скејтборда статичка сила трења тј
Једначина кретања дечака је
услов да се дечак не креће у односу на скејт
Убрзање скејтборда је једнако убрзању дечака, пошто се крећу заједно па закључујемо да у граничном случају када убрзање скејтборда постане једнако
\(a=\mu \cdot g\),
дечак почиње да проклизава по њему.
Правац силе трења клизања је увек тангента на додирну површину. Битно је нагласити да је динамичка сила трења клизања увек усмерена супротно релативној брзини тела, а не супротно брзини тела коју видимо из неког непокретног система, нпр оног који је везан за под. Ако се тело креће по поду који мирује, онда је брзина подлоге једнака нули, гледано из система референције везаног за под, па релативну брзину тела изједначавамо са брзином коју видимо.