Осцилације у подацима¶

Такође смо могли да приметимо значајне дневне осцилације у објављиваним бројевима новозаражених коронавирусом. Такве осцилације могу настати из разних техничких разлога у поступку регистровања и извештавања на различитим нивоима.

На пример, када се у неком колективу открије први заражени, често се деси да се у наредна два дана региструје значајан број новозаражених из тог колектива, али се нису сви заразили за два дана. То ствара краткотрајне скокове у броју новозаражених који нису одраз толико великих осцилација у стварности, већ су те осцилације последица начина откривања новозаражених кроз праћење контаката.

Такође се дешава да се, на пример, понедељком региструје мањи број новозаражених. Вероватан разлог је да се викендом посета лекару често одлаже за понедељак уколико није хитан случај. Онда пацијенти који се прегледају и тестирају у понедељак треба прво да сачекају резултате теста и не стигну да буду урачунати у пресек који се објављује у понедељак.

Графикон на слици 1 приказује званичне податке за Србију током септембра 2020. године и јасно се види како се сваког понедељка дешава пад регистрованог броја новозаражених, а такође видимо како наилазе и друге дневне осцилације, које су биле нешто израженије у другој недељи септембра.

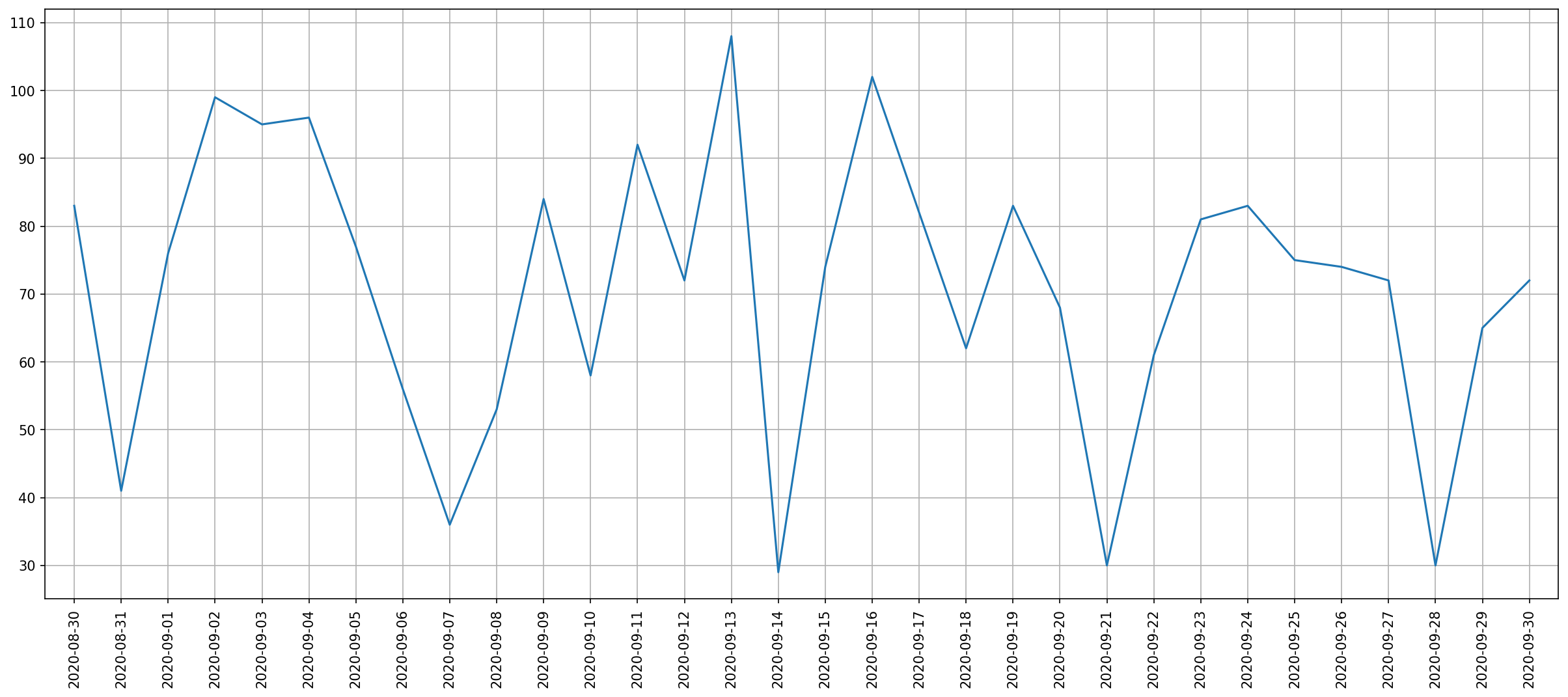
Слика 1. Осцилације регистрованог броја новозаражених – Србија, септембар 2020.¶

Осцилације у званичним бројевима могу настати и у ланцу извештавања. На пример, у дневним извештајима Светске здравствене организације се дешавало да се појави нула новозаражених за неку земљу за одређен датум. Разлог за то може бити што нису увек синхронизовани дневни пресеци стања које праве државе и дневни пресеци стања које прави Светска здравствена организација (СЗО). Тако се догоди да између два извештаја СЗО нису стигли нови подаци из неке земље. Тада укупан регистрован број заражених у два узастопна извештаја СЗО остане исти за ту земљу, а то аутоматски значи да у другом извештају мора да се прикаже нула новозаражених.

Када се тако неочекивано појави нула код података за неку земљу, онда обично имамо и повећан број новозаражених наредног или претходног дана. Број новозаражених који је пропуштен да буде регистрован у дану где је приказана нула најчешће је преливен у претходни или наредни дан. Сва та преливања између дана се могу дешавати и на нижим нивоима у ланцу извештавања унутар земаља и градова у зависности од тога како је организован процес извештавања. Све то додатно доводи до дневних осцилација које нису одраз стварних осцилација у броју заражених.

Због разних могућих узрока дневних осцилација у броју регистрованих заражених особа, а које не осликавају стварне осцилације у броју заражених, не треба доносити закључке само на основу промена у односу на претходни дан. Увек треба посматрати податке током више дана да би се могао направити некакав заључак о динамици ширања заразе. Ако је изражен недељни ритам осцилација, добро је посматрати недељне просеке или збирове.

У праћењу епидемије COVID-19 један од показатеља је и 14-дневни збир регистрованог броја заражених. Тиме се уједно добија апроксимација за број активно оболелих случајева ако се претпостави да од позитивног теста болест у просеку траје 14 дана.

Вероватно најчешћи пропуст који нам се дешава у интерпретацији дневних података је пренаглашен фокус на томе да ли имамо раст, пад или стагнацију броја новозаражених у односу на претходни дан.

Графикон са слике 1 заправо показује да је током септембра 2020. године био релативно стабилан број новозаражених уз уобичајене дневне осцилације. На жалост, када се сваког поподнева објави нови епидемиолошки пресек рефлексно се фокусирамо на управо објављене бројеве и колико су се променили у односу на претходни дан. Са таквим фокусом изгледа као да се епидемиолошка ситуација драстично мења из дана у дан, што тог септембра није био случај.

Наравно, постоје и другачији примери, где се иза дневног раста крије експлозивни почетак епидемиолошког таласа, а не краткотрајни шпиц. Или се иза дневног пада крије прелазак епидемиолошког таласа у силазну фазу, а не затишје. Главно је разумети да треба да гледамо промене за више дана да бисмо доносили закључке о тренду.

Корисна додатна информација је и посматрање података по мањим територијалним целинама. На пример, дешава се понекад да се у неколико већих градова сусретну истог дана шпицеви или затишја, што производи скок или пад у збирним подацима за целу земљу. Ако знамо да је то позадина скока или пада, онда можемо претпоставити да ће промена бити краткотрајна.

Другачији пример би био да је један од највећих градова у земљи ушао у експоненцијални раст и да је достигао ниво да то значајно утиче на повећање укупног броја заражених у земљи. Ако знамо да је таква позадина повећања, онда сасвим могуће улазимо у нови епидемиолошки талас.

Пример једне веће земље¶

За следећи пример ћемо узети податке за неку већу земљу, у конкретном случају Русију. У већој земљи процес ширења и након тога опадања броја заражених дуже траје. Такође због више великих насељених места збирни подаци су статистички уједначенији.

На слици 2. је приказана крива дневног броја заражених за Русији према подацима СЗО. Покривен је период од средине марта када су се појавили први случајеви заразе, па до краја јуна, када је први епидемиолошки талас већ био у јасном опадању.

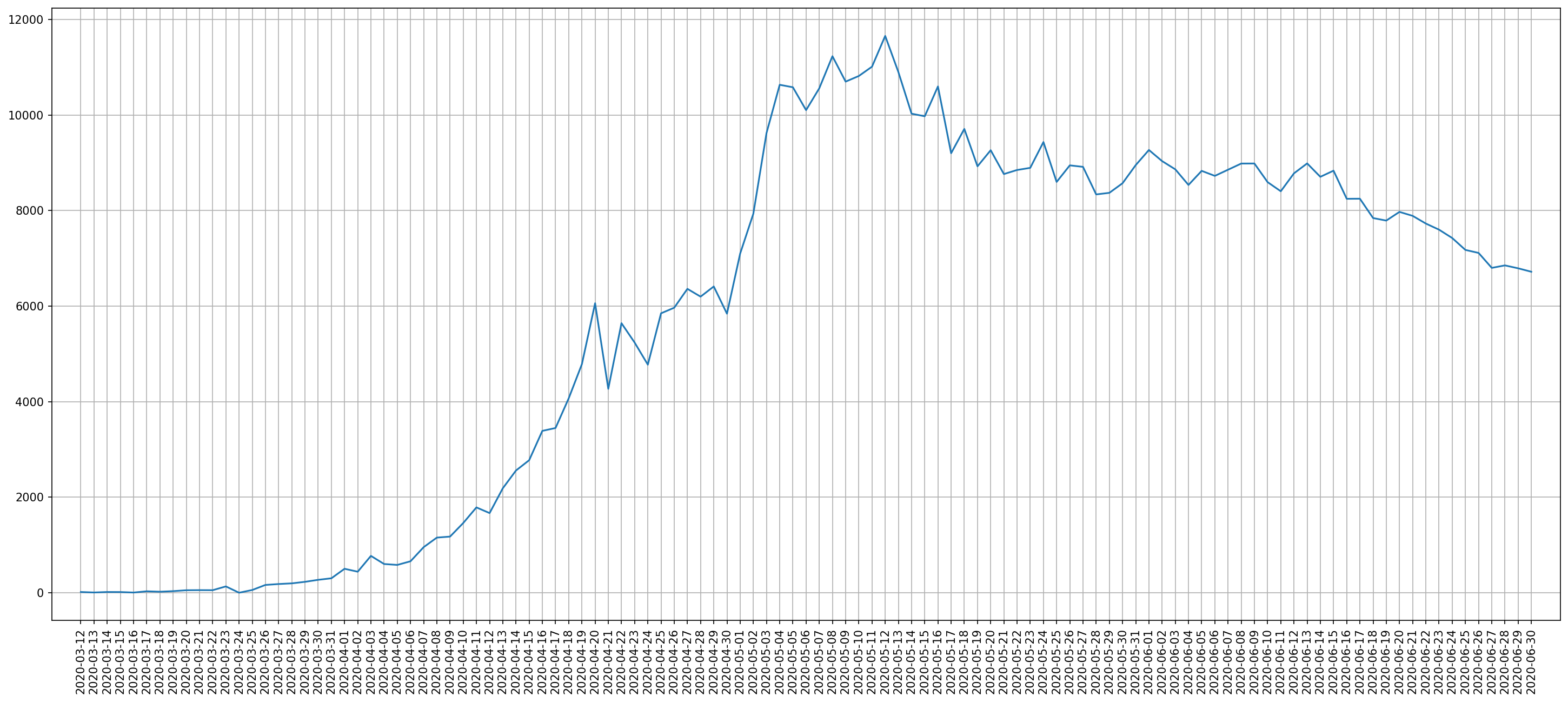
Слика 2. Дневни број новозаражених – Русија, март-јун 2020.¶

Приметимо прво да је 24. марта СЗО евидентирала нула новозаражених у Русији, што је пример случаја о коме смо говорили. Постоје дани када се тако нешто десило и за Србију и за многе друге земље. У конкретном случају за Русију видимо да је 23. марта било нешто више регистрованих случајева, конкретно 132. Касније су подаци кориговани: за 23. март је кориговано на 61, а за 24. март на 71, што у збиру даје истих 132. Овај случај одговара нашем ранијем објашњену могућих техничких разлога за преливање бројева из дана у дан.

Такође видимо велике дневне осцилације након 20. априла што тешко да може одговарати реалним скоковима у броју новозаражених већ, највероватније настаје из техничких разлога о којима смо причали.

Ако желимо да умањимо шум дневних осцилација, а сматрамо да би нам седмодневни просек сувише смањио прецизност, можемо користити трансформацију која укључује три дана, текући и два суседна. Пошто у осцилацијама има доста преливања управо између суседних дана, тиме можемо добити добар баланс равнања осцилација и задржавања прецизности.

Најчешће се користи следећа формула

при чему је важно да буде

Та једнакост значи да смо нешто прелили из једног у други дан, али укупно нисмо ништа додали нити одузели.

На слици 3. је приказан резултат трансформације

Наведену формулу не можемо да применимо на први и последњи датум, јер не знамо \(f(t-1)\) односно \(f(t+1)\). У овом случају смо опсег који посматрамо просто скратили за по један дан са обе стране, јер нам рубни датуми нису посебно значајни, па нам је тако било најједноставније.

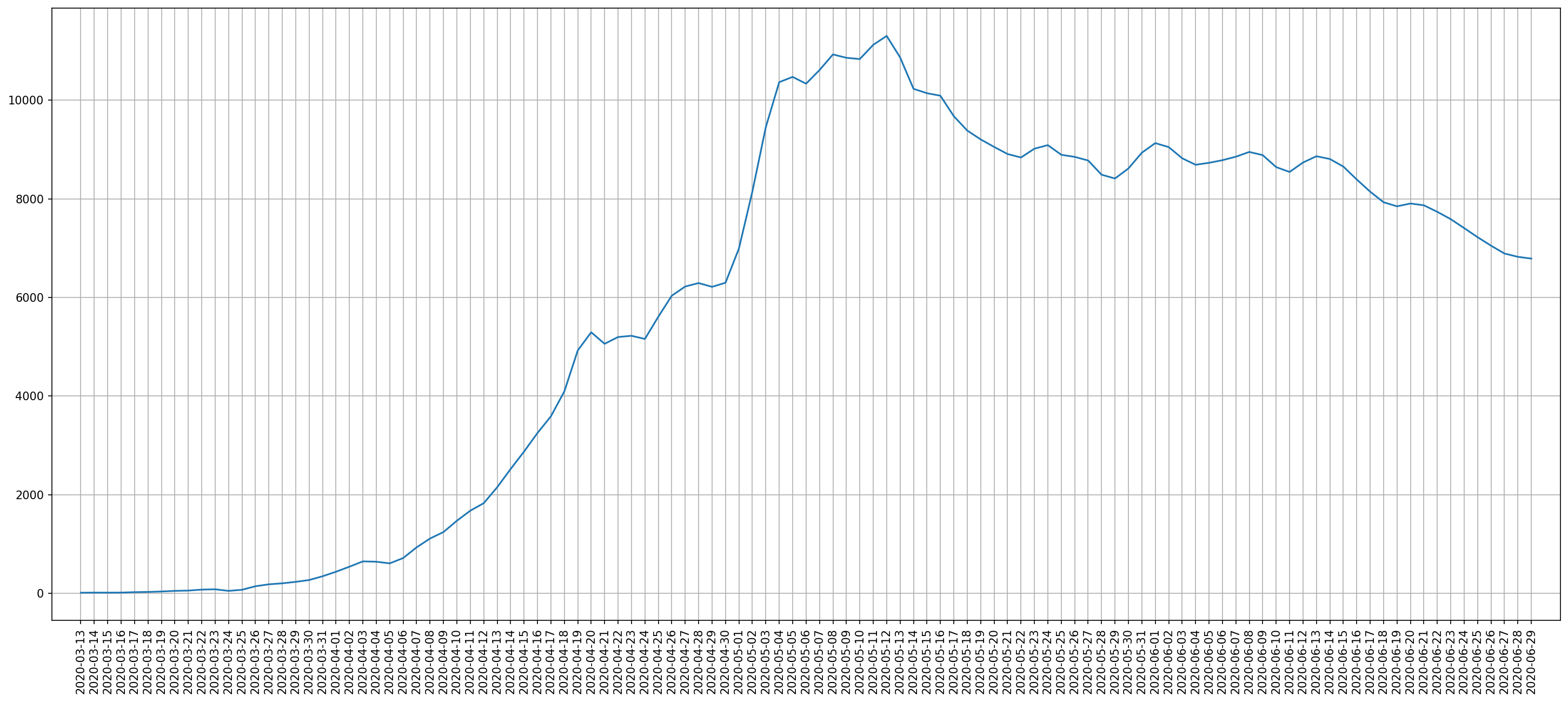
Слика 3. „Углачана” крива за дневни број новозаражених – Русија, март-јун 2020.¶

Коришћење логаритамске поделе \(y\) осе¶

Видимо да крива на слици 3. има више фаза, а у периоду до 20. априла се дешава раст који личи на експоненцијални.

Питамо се да ли је то експоненцијални раст. Ми обично лако приметимо када је крива у неком делу линеарна, али је мање очигледно где се дешава експоненцијални раст.

Једноставна техника да експоненцијални раст учинимо уочљивијим је да \(y\) осу пребацимо у логаритамску поделу (слика 4).

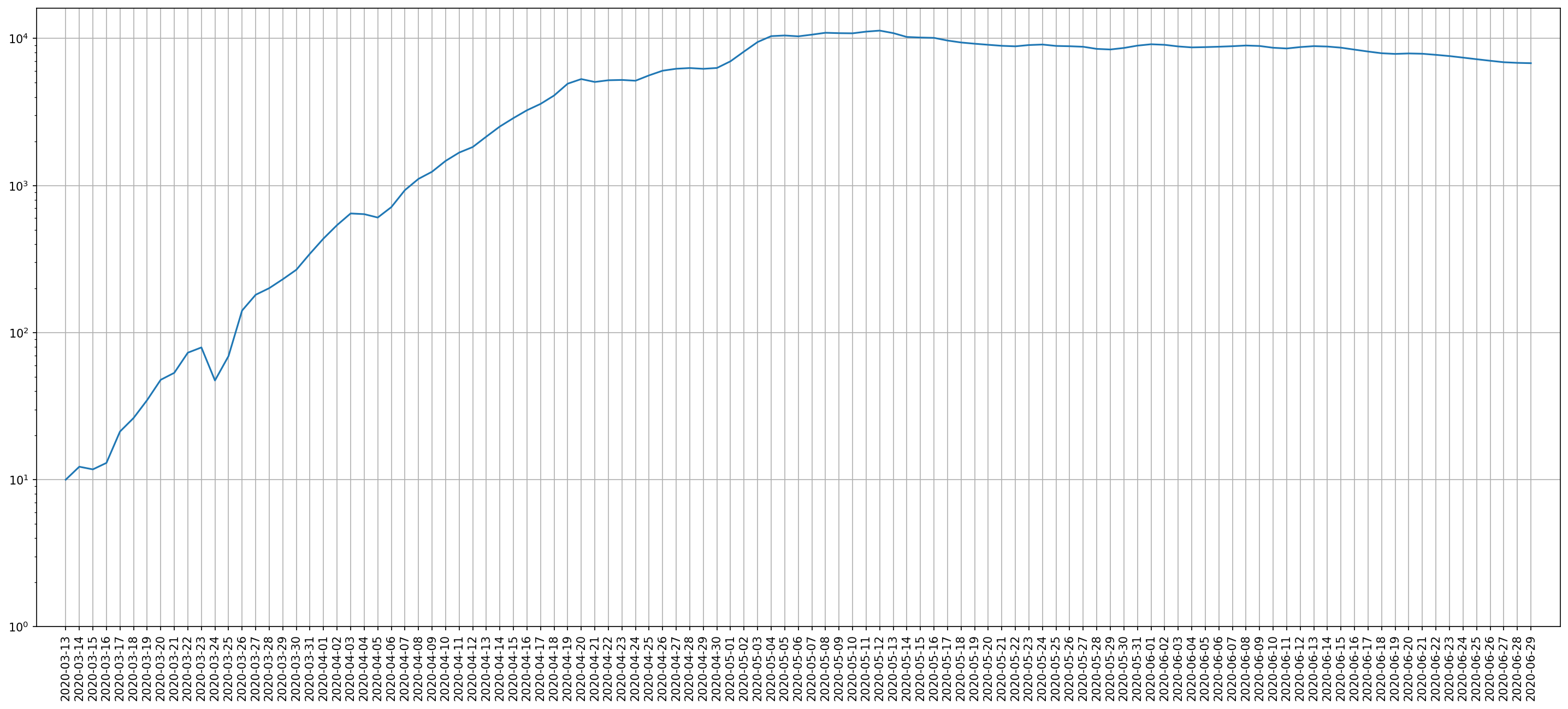
Слика 4. Дневни број новозаражених у логаритамској расподели са основом 10¶

Логаритамска подела значи да се у правилним корацима вредност на \(y\) оси удесетостручава или удвостручава уместо да се равномерно увећава.

Заправо, вредности по \(y\) оси експоненцијално расту у односу на положај тачке на оси. Са друге стране положај тачке на \(y\) оси логаритамски расте у односу на вредност коју тачка представља, због чега се подела зове логаритамска.

Прелазак на логаритамску поделу је уобичајена опција код рачунарских алата који се користе за израду графикона.

На слици 4. су на \(y\) оси истакнути степени десетке: \(10^0=1\), \(10^1=10\), \(10^2=100\) \(\dots\)

Уочљив пад 24. марта је од оне нуле која је у извештају СЗО писана за 24. март. Пад је је остао приметан и након што смо криву „углачали”. Тај пад 24. марта је слабије уочљив на слици 3. јер се дешава у зони малих вредности и промене се једва виде.

Карактеристично за логаритамску поделу \(y\) осе је да су релативни односи једнако уочљиви и код малих и код великих вредности. На пример, дупло повећање или дупло смањење је на логаритамској подели једнако уочљиво и у зони малих и у зони великих вредности.

Друго важно својство за логаритамску поделу \(y\) осе је да крива експоненцијалне функције постаје права линија. То значи да експоненцијални раст у логаритамској подели графички изгледа исто као линеаран у уобичајеној подели \(y\) осе.

На слици 4. можемо уочити да до 20. априла крива има стабилан нагиб уз одређене осцилације. Нагиб се у неким деловима смањује, али се не приближава хоризонтали. То значи да можемо рећи да се до 20. априла у Русији дешавао експоненцијали раст броја регистрованих новозаражених, са мањим променама стопе раста.

Када имамо дужи период експоненцијалног раста броја регистрованих новозаражених можемо бити прилично сигурни да се и стварни број заражених, који никада не можемо прецизно измерити, такође ширио експоненцијалном брзином.

Ако желимо да посматрамо динамику удвостручавања, логаритамску поделу \(y\) осе треба да прикажемо са степенима двојке, тј. са основом \(2\) (слика 5).

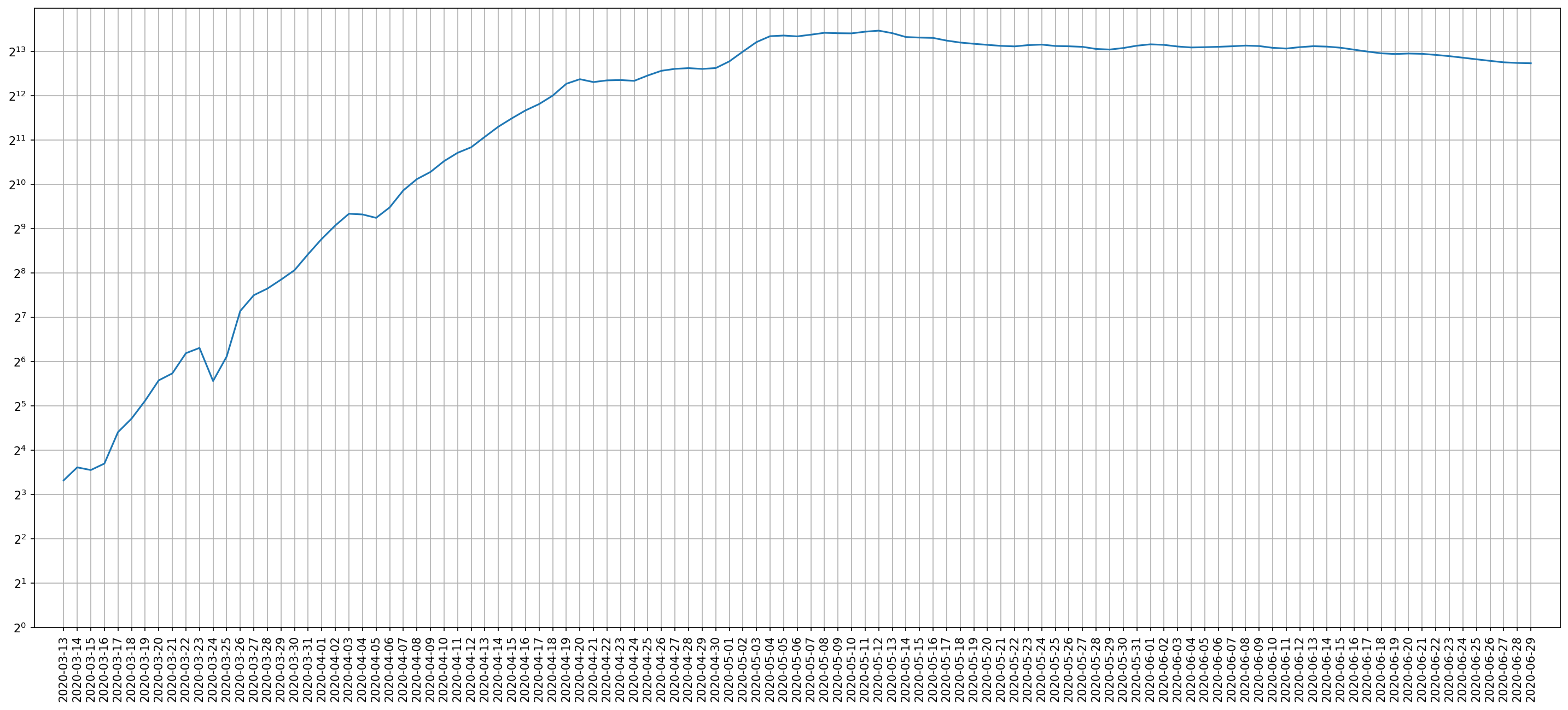
Слика 5. Дневни број новозаражених у логаритамској расподели са основом 2¶

Оријентације ради, \(2^{10}=1024\), тј. мало више од \(10^3\).

На слици 5. можемо приметити да се у периоду до 21. априла дневни број регистрованих случајева заразе у Русији удвостручавао на \(3\) до \(5\) дана, ако изузмемо периоде осцилација.

Након тога се раст значајније успорио, нагиб криве почиње да се прибижава хоризонтали и на крају крива креће да опада. И у силазном делу видимо експоненцијални пад јер имамо стабилан нагиб који се не враћа према хоризонтали, али је стопа тог пада много блажа него што је била стопа раста.

Просечне дневне стопе раста за периоде удвостручавања од \(3\), \(4\) и \(5\) дана су редом \(\sqrt[3]{2}-1\approx 26\%\), \(\sqrt[4]{2}-1\approx 19\%\) и \(\sqrt[5]{2}-1\approx 15\%\). Ако знамо дневну стопу раста \(r\) и имамо претпоставку колики је просечан генерацијски интервал \(Т\) лако рачунамо ефективни репродукциони број \(R\). Да се подсетимо, формула је

где је са \(p\) означен период удвостручавања.

Ако претпоставимо да је просечан генерацијски интервал био \(5\) дана, онда се у периоду експлозивног раста репродукциони број \(R\) кретао између \(2^{5\over 5} = 2{,}0\) и \(2^{5\over 3}\approx 3{,}2\).

Када епидемија крене да расте важно је да пратимо период удвостручавања. Период удвостручавања лако очитава на логаритамској подели \(y\) осе са основом \(2\). Када период удвостручавања устали на малом броју дана, односно када се репродукциони број устали изнад један, то треба да буде разлог за забринутост. Чак и у случају када дневни ниво новозаражених сам за себе још увек није алармантан. Заправо је то главни случај који је потребно препознати и на време реаговати. Када епидемиолошки талас достигне врхунац свима је јасно шта се дешава.

Устаљено кратак период удвостручавања, односно репродукциони број који се усталио изнад јединице, значи да су се стекле околности које погодују интензивнијем преносу заразе. Ако не предузмемо ништа да се те околности промене остаће висок репродукциони број и кратак период удвостручавања. А свако лако може да израчуна колико брзо ће се епидемија ширити ако се задржи дати период удвостручавања.