Процедуре¶
Пројекти које ћемо проучавати у овом поглављу представљају надоградње пројеката из претходних поглавља и имају сложену структуру. Да бисмо се лакше изборили са том сложеношћу и да бисмо их брже и лакше тестирали разделили смо их у процедуре. Свака од процедура извршава одређену функцију, а једна скрипта, главни програм, их позива и повезује у јединствену целину.
 Проучи следеће примере пројеката¶
Проучи следеће примере пројеката¶
Пример 1 - Пројекат Мрежа_квадрата¶
Цртање хоризонталних линија
Да бисмо нацртали хоризонталну линију (паралелну х оси) потребно је да повежемо све тачке које имају исту вредност координате у. На пример, ако је у=0 нацртаћемо саму х осу. На почетку поставимо оловку на леви руб екрана у тачку (-240,0), спустимо је да би остављала траг и пошаљемо да клизи до тачке (240,0). Тамо је подигнемо и можемо да пређемо на цртање следеће линије.
Ако желимо да нацртамо све хоризонталне линије чија је у координата број који се завршава цифром 0 (дељив са 10) понављаћемо претходно описани поступак за у=180, 170, …,-180.

Да би сам поступак био прегледнији, издвојићемо инструкције за цртање једне хоризонталне линије у засебну целину – процедуру, коју ћемо по потреби позивати.
Један од начина да се у Скречу реализују процедуре и тако сложени алгоритми изделе на више једноставних је коришћење порука, исти механизам који смо већ упознали када смо синхронизовали акције различитих ликова или омогућавали једном лику да реагује на различите догађаје.
На следећој слици приказан је овакав начин организације циклуса у коме се цртају хоризонталне линије. У телу петље је позив процедуре који се остварује инстукцијом разгласи и чекај. Овај начин слања поруке зауставља извршавање самог програма док се не изврши блок инструкција прикључен примању одговарајуће поруке. Да смо употребили инструкцију разгласи (без чекања), петља би се извршила потребан број пута, али небисмо видели цртање.
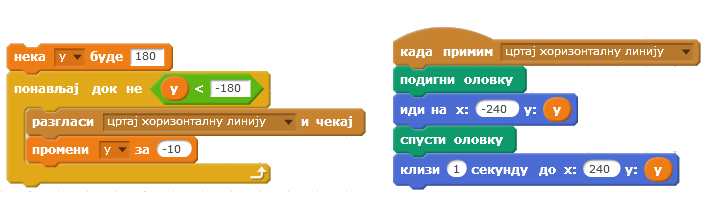
Цртање вертикалних линија
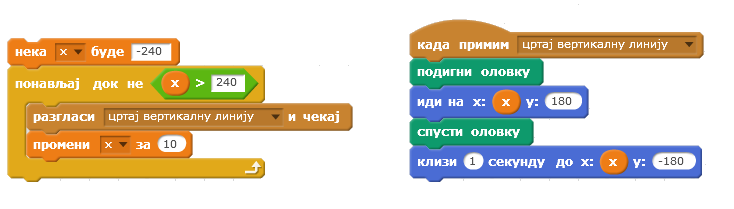
Слично цртању хоризонталне линије, да бисмо нацртали вертикалну линију потребно је да повежемо све тачке које имају исту вредност координате х. На почетку поставимо оловку на горњи руб екрана, на пример у тачку (0,180), спустимо је да би остављала траг и пошаљемо да клизи до тачке (0,-180). Тамо је подигнемо и можемо да пређемо на цртање следеће линије.
Ако желимо да нацртамо све вертикалне линије чија је х координата број дељив са 10) понављаћемо претходно описани поступак за х=-240, -230, …,240.
Да бисмо упамтили слику мреже квадрата добијених цртањем хоризонталних и вертикалних линија на овај начин потребно је да на урадимо десни клик на позорницу. Појавиће се опција save picture of stage која омогућава да се слика позорнице упамти као позадина.
Главни програм који црта мрежу хоризонталних и вертикалних линија приказан је на следећој слици.
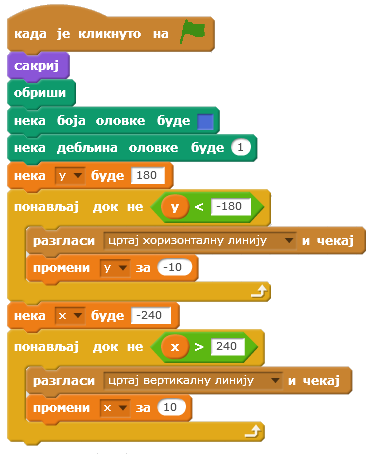
Упамтите цео појекат под називом Мрежа квадрата.
Пример 2 - Пројекат Разне_мреже¶
Ако желимо да уопштимо претходни програм и користимо га за цртање мреже већих или мањих квадрата, као и за цртање мреже која не почиње обавезно
у горњем левом углу екрана и завршава се у доњем десном углу, увешћемо променљиве Х мин, Х мах, У мин, У мах и корак.
Оне ће дефинисати горње лево теме мреже (Х мин, У мах), доње десно теме мреже (Х мах, У мин) и величину квадрата у мрежи.
Полазне вредности ћемо задавати коришћењем инструкције 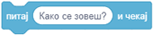 .
.
Тако можемо изменити пројекат Мрежа квадрата који црта само једну мрежу у општији пројекат Разне мреже који може да црта различите мреже у зависности од улазних података. Осим побројаних променљивих увели смо и променљиву крај која је иницијално постављена на 0, а мења се у случају да корисник више не жели да користи програм. Било који одговор осим „да“ не мења њену вредност.
Када корисник на Крај (да/не)? одговори са „да“, променљива мења своју вредност у 1 што је услов за излазак из циклуса и програм се прекида.
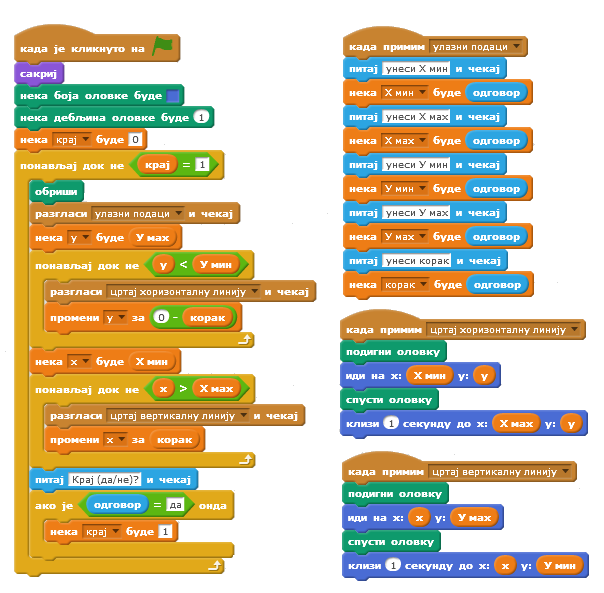
Резултати извршавања пројекта Разне мреже за различите вредности улазних променљивих приказани су на следећој слици. Последњи резултат приказан је после корисниковог одговора да жели крај.
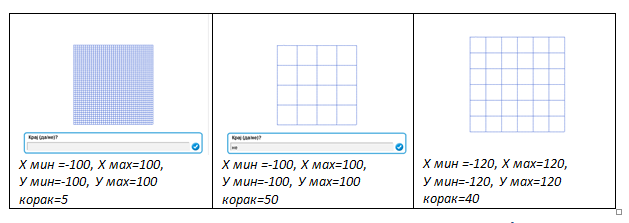
Пример 3 - Пројекат Геометријске_фигуре3¶
Сваком од низова наредби за цртање многоуглова придружићемо име – односно увешћемо нове инструкције: Цртај троугао, Цртај квадрат, Цртај петоугао, Цртај шестоугао.
Увођење сопствених наредби
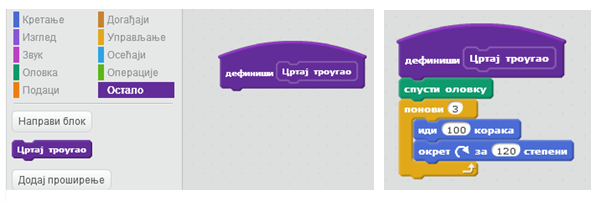
У групи наредби Остало кликни на дугме Направи блок. Појавиће се дијалошки прозор који омогућава креирање сопствених наредби. У пољу за назив наредбе упиши Цртај троугао и потврди кликом на дугме У реду.

У палети блокова појавиће се нови блок Цртај троугао, а у области скрипти нови почетни блок Дефиниши Цртај троугао којем треба придружити низ блокова за цртање троугла.
Слично треба направити наредбе за цртање квадрата, петоугла и шестоугла и затим их користити у свом програму за цртање.
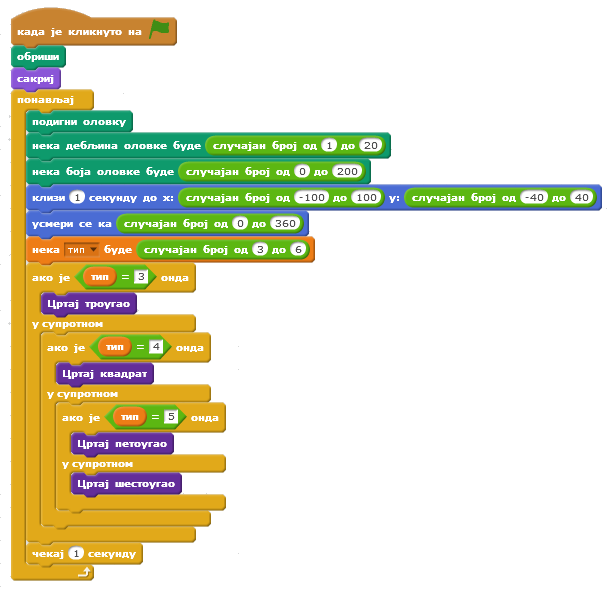
Ми ћемо у главном програму у бесконачној петљи постављати дебљину и боју оловке, као и позицију и смер лика који црта на случајан начин, а затим генерисати вредност променљиве тип између 3 и 6. У зависности од вредности ове променљиве главни програм ће позивати једну од процедура (3 – Цртај троугао, 4 – Цртај квадрат, итд). Главни програм приказан је на следећој слици. Упамтите овај пројекат по називом Геометријске фигуре 2.
Унапређење пројекта
Пример 4 - Пројекат Геометријске_фигуре4¶
Како су процедуре за цртање многоуглова које користи пројекат Геометријске фигуре 2 веома сличне, направићемо нову процедуру Цртај многугао која би цртала сваки од наведених правилних многоуглова ако јој се проследи број страница, означимо га са n. Петља за цртање би се понављала n путa, а спољашњи угао би износио 360/n.
Да бисмо направили процедуру која различито ради у зависности од прослеђеног броја страница многоугла потребно је да из приручног менија који добијемо десним кликом на нови блок (1) или његову дефиницију (2) изаберемо опцију Уреди. Отвориће се дијалошки прозор Уреди блок, у коме треба отворити списак опција Могућности (3) и изабрати опцију Додај нумерички улаз (4). Уз назив новог блока појавиће се поље у коме пише number1 (5), уместо које треба уписати назив – лабелу која одговара процедури. Код нас ће то бити лабела број страница (6).
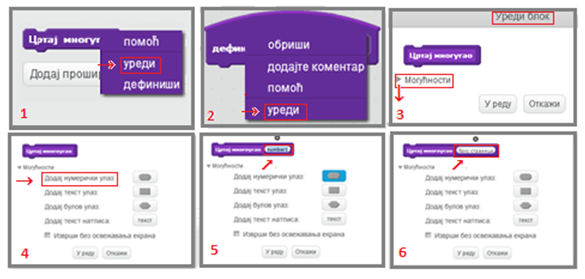
Назив „број страница” који смо унели у заглавље дефиниције процедуре Цртај многогугао назива се параметар.
Ако желимо да процедура Цртај многоугао црта правилне многоуглове са различитим бројем страница, број страница многоугла ћемо задати као аргумент новоуведене наредбе. Тај аргумент ће заменити свако појављивање параметра „број страница” у процедури. Можемо да кажемо да је параметар именовани чувар места за аргумент. Параметар број страница који се појављује у заглављу процедуре поставља се на места на којима је то потребно у телу процедуре исто као што се поставља било која променљива у одговарајући блок – превлачењем.
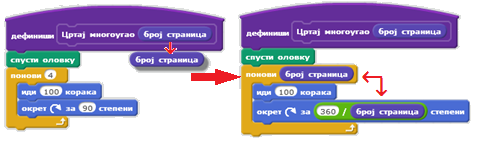
Ако желимо да учинимо процедуру још универзалнијом и додамо јој могућност да црта правилне многоуглове са различитим дужинама страница, поновићемо поступак и додати још један нумерички улаз. Овом параметру даћемо назив дужина странице. На следећој слици приказана је скрипта која дефинише процедуру Цртај Многоугао која има два параметра.
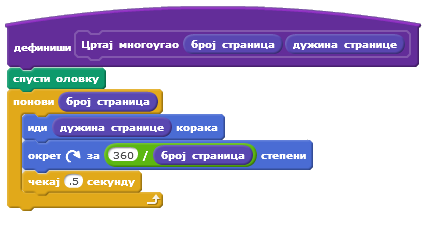
Главни програм у бесконачној петљи позива ову процедуру која црта правилни многоугао у складу са прослеђеним аргументима и после 1 секунде га брише. Аргументи се генеришу на случајан начин. Број страница може бити од 3 до 8, а дужина од 10 до 100. У петљи се такође на случајан начин генеришу дебљина и боја оловке. На следећој слици приказана је скрипта главног програма.
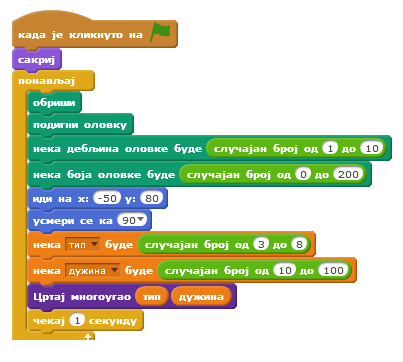
Пример 5 - Пројекат Мали_математичар4¶
Пројекат Математичар 4 надограђује пројекат Математичар 2 који ради са бројевима од 1 до 9. За надоградњу је потребно лику Знак додати још 2 костима „–„ за одузимање и „:“ за дељење. Треба изменити и скрипту која описује понашање математичара када се кликне на њега.

Подразумева се да корисник зна шта су негативни бројеви. Код дељења се треба постарати да резултат буде цео број и избећи дељење нулом. Да бисмо избегли проблеме код дељења, ако се приликом генерисања операције открије да је то дељење позваћемо процедуру Дели, а у свим осталим случајевима радићемо на начин као што је то било решено у претходним примерима.
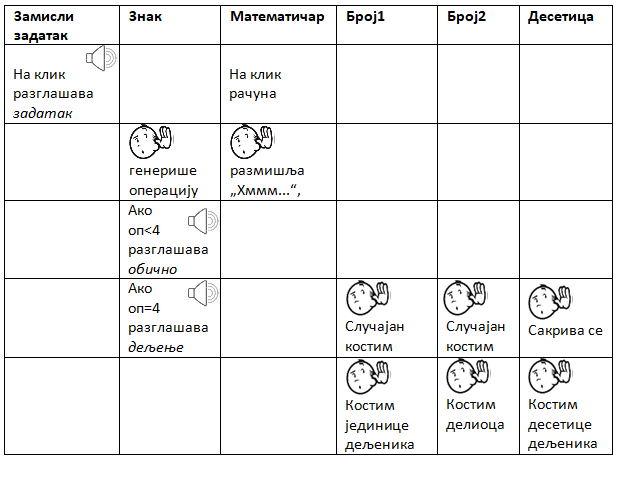
Дакле, када се кликне на дугме Замисли задатак оно шаље поруку „задатак” на коју реагују Математичар и Знак. Математичар размишља „Хммм…“, а Знак генерише случајан број од 1 до 4 и приказује се у одговарајућем костиму (1 – множење, 2 – сабирање, 3 – одузимање, 4 – дељење).
За све операције осим дељења Знак шаље поруку „обично”, а ако се ради о дељењу позива процедуру „Дели” која се завршава слањем поруке „дељењe”. На поруке које шаље Знак реагују Број1 и Број2 .
Ликови Број1 и Број2 на поруку обично реагују као у претходним верзијама пројекта Математичар, односно приказују се у једном од случајно изабраних костима од 1 до 9. Међутим, ако се ради о дељењу, начин постављања задатка је сасвим другачији, иде се од резултата ка бројевима који га образују. Наиме, у процедури Дели генеришу се два случајна броја из интервала [1,9]. Први од њих додељује се променљивој количник, а други променљивој делилац. Они се множе и формирају променљиву дељеник.
Вредност променљиве дељеник додељује се лику Број1, а вредност променљиве делилац лику Број2. Тако математичар дељењем дељеника са делиоцем сигурно добија целобројну вредност из интервала [1,9].
Овакав начин генерисања задатака од резултата ка операндима користићемо и у другим пројектима како бисмо обезбедели да корисник добије задатак који уме да реши, рецимо да при одузимању не добије негативан резултат или да резултат множења буде до 50, а да фактори могу да буду и већи бројеви и слично.
Оно што се јавља као нови проблем у оваквом решењу задатка је што ће дељеник вероватно бити двоцифрен број, а може се завршавати и цифром 0 која у претходним пројектима није била укључена у костиме за Број1. Овај проблем решавамо тако што уводимо још један лик, умножак лика Број1 који смо назвали (цифра) Десетица, а лику Број1 додајемо нулу као 10. костим. Лик Дестица се не види, појављује се једино када Знак пошаље поруку дељење, а претходно израчунати дељеник је двоцифрен број (што детектује променљива број цифара). Тада се Десетица (цифра десетица дељеника) појављује лево од лика Број1 који добија вредност цифре јединица дељеника.
За издвајање цифара дељеника користимо операцију  која издваја знак са наведеним редним бројем из стринга.
која издваја знак са наведеним редним бројем из стринга.
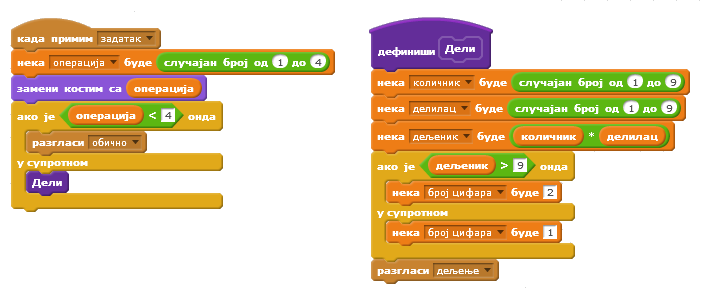
Како Скреч врши аутоматску конверзију података из нумеричких у стринг и обратно, цифре вишецифрених бројева се сасвим једноставно издвајају овом операцијом и засад није неопходно објашњавати шта је целобројно дељење ни која операција враћа остатак при целобројној деоби. На следећим сликама приказане су скрипте придружене лику Знак и бројевима.

 Покушај¶
Покушај¶
Вежба 1¶
Вежба 2¶
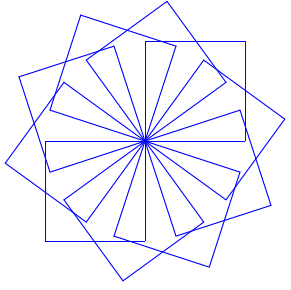
Направи процедуру Квадрат2 са параметрима: координате х и у горњег левог темена, дужина странице a и правац прве странице угао коју исцртава процедура. Затим креирај скрипту који позива више пута ову процедуру и црта 10 квадрата са заједничким горњим левим теменом, истих страница тако да је правац сваке следеће прве странице заротиран 36 стeпени у односу на правац прве странице претходног квадрата.
Вежба 3¶
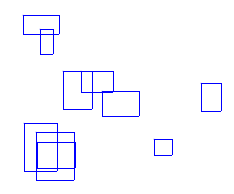
Направи процедуру Правоугаоник са параметрима: координате х и у горњег левог темена и дужинама страница а и b. Процедура треба да црта правоугаоник са страницама дужине а паралелним х оси, а страницама дужине b паралелним у оси. Затим креирај скрипту који позива више пута ову процедуру и црта правоугаонике са аргументима који се задају на случајан начин, слично као на следећој слици.
 Уради неки од следећих пројеката¶
Уради неки од следећих пројеката¶
Пројекат 1 - Аритметика¶
Направи процедуре које треба повезати у пројекат Аритметика. Процедуре треба да тестирају познавање сабирања, одузимања, множења и дељења. Пројекат треба да има интерфејс као на следећој слици.
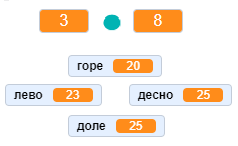
У горња два монитора, између којих се налази знак аритметичке операције, треба уписати бројеве генерисане на случајан начин, а у доња четири бројеве који који би могли бити резултат, при чему је само један од њих тачан. Играч бира одговор за који мисли да је тачан помоћу дирке са одговарајућом стрелицом. Ако је одговор тачан, добија одговарајућу поруку и увећава му се број поена за 1. Ако је одговор нетачан, добија одговарајућу поруку и умањује му се број поена за 1. Тестирање се завршава када одговори на 20 питања уз поруку на колико је процената питања тачно одговорио.
Пројекат формирај на следећи начин:
1) У процедури Сабирање на случајан начин треба генерисати два броја, збир c из интервала [10,20] и први сабирак a из интервала [1,15]. На основу њих формирати други сабирак b = c - a и три погрешна резултата из интервала [c-3,c+3].
2) У процедури Одузимање на случајан начин треба генерисати два броја, Умањеник a из интервала [10,20] и умањилац b из интервла [1,a-2]. На основу њих формирати разлику c = a - b и три погрешна резултата из интервала [c-2,c+2].
3) У процедури Множење на случајан начин треба генерисати два фактора из интервала [2,9]. На основу њих формирати производ c = a * b и три погрешна резултата из интервала [c-10,c+10]. Побринути се да погрешни резултати буду већи од оба фактора (нпр. ако се за факторе 2 и 3 генерише погрешан одговор 2, поновити генерисање).
4) У процедури Дељење на случајан начин треба генерисати два броја, количник c из интервала [2,9] и делилац b из интервала [2,9]. На основу њих формирати дељеник a = b * c и три погрешна резултата из интервала [c-3,c+3].
5) У главном програму треба променљивим поени и покушаји поставити вредност 0. Затим у петљи која ће се понављати све док број поена не буде 20 генерисати аритметичку операцију, позвати одговарајућу процедуру и добијене операнде поставити у одговарајуће мониторе уз рачунску операцију, а тачан и 3 погрешна одговора распоредити на случајан начин у мониторе за одговоре. (Можете и распоређивање одговора решити у засебној процедури.)
Затим програм треба да прихвати одговор корисника и, у зависности од тога да ли је тачан или, прикаже одговарајућу поруку и промени променљиве поени и покушаји. По изласку из петље програм треба да саопшти на колико је процената постављених задатака корисник тачно одговорио.
Пројекат 2 - Близанци¶
Направи процедуре које треба повезати у пројекат Близанци.
Процедура Провера треба да проверава да ли је број који се задаје као параметар прост.
Процедура Формирај треба да формира листу Прости у коју ће уписати све просте бројеве из интервала [2,1000].
Главни програм треба да приказује све бројеве близанце (просте бројеве који се разликују за 2) из интервала [2,1000].


 Шта смо научили
Шта смо научили -
-  ,
, 